Prediction of Vapor-Liquid Equilibrium for a Non-Ideal Binary Mixture Based on the Azeotropic Condition

Larry K. Jang; You-Im Chang

doi:https://doi.org/10.47739/2333-6633/1039

Prediction of Vapor-Liquid Equilibrium for a Non-Ideal Binary Mixture Based on the Azeotropic Condition

Short Communication | Open Access | Volume 3 | Issue 2

Article DOI : https://doi.org/10.47739/2333-6633/1039

Larry K. Jang^1* You-Im Chang²

^1. Department of Chemical Engineering, California State University, USA
^2. Department of Chemical Engineering, Tunghai University, Taiwan

+ Show More - Show Less

Corresponding Authors

Larry K. Jang, Department of Chemical Engineering, California State University Long Beach, CA 90840-5103, USA

ABSTRACT

A simplified procedure for predicting vapor-liquid equilibrium of a non-ideal binary solution based on the known azeotropic condition under constant pressure is developed in this work. First, liquid-phase activity coefficients of both components at the azeotropic condition under a certain system pressure are calculated and then substituted into two-parameter activity coefficient models (such as Van Laar, Margules, and Wilson). The model parameters can be easily solved directly or with simple numerical procedures. Assuming that these model parameters are insensitive to temperature, one may further calculate the activity coefficients, the bubble point and dew point temperatures as well as equilibrium vapor-phase compositions at any liquid- phase compositions under the given system pressure. The results of calculation indicated that the predicted vapor-liquid equilibrium agrees very well with both published data as well as that calculated by more elaborated procedures in the literature. The non- ideal binary solution containing 1-propanol and water at 1 atm (101.325kPa) is chosen to illustrate the procedure developed in this work.

KEYWORDS

Vapor-Liquid Equilibrium (VLE)
Activity Coefficient
1-Propanol/Water
Van Laar
Margules
Wilson
Azeotrope

CITATION

Jang LK, Chang YI (2017) Prediction of Vapor-Liquid Equilibrium for a Non-Ideal Binary Mixture Based on the Azeotropic Condition. Chem Eng Process Tech 3(2): 1039.

THEORY

For low to moderate total pressure (PT ) when the vapor phase can be assumed to be an ideal gas, the partial pressure (Pi , i = 1, 2) of each component above a non-ideal homogeneous binary liquid mixture can be expressed by the modified Raoult’s law [1(a)]:

$P_{1}= P_{T} Y_{1}=\gamma_{1} X_{1}P_{1}^{sat}(T)$ (1)

$P_{2}= P_{T} Y_{2}=\gamma_{2} X_{2}P_{2}^{sat}(T)$ (2)

Xi is the mol fraction of component i in the liquid phase, Yi is the mol fraction of component i in the vapor phase, Pi sat is the vapor pressure of pure species i at the system temperature, PT is the total pressure of the binary system, and γi is the activity coefficient of component i in the liquid phase (γi = 1.0 for an ideal solution). When the sum of partial pressures Pi‘s equals the applied pressure, the mixture boils and the temperature is called the bubble point temperature at liquid composition Xi (and also the dew point temperature at vapor composition Yi ) .

There are many theoretical and empirical models of excess Gibbs free energy (GE) for estimating the activity coefficients of components in non-ideal liquid solutions. In the literature, elaborate procedures for computing bubble point (B.P.) and dew point (D.P.) temperatures of non-ideal solutions are available [1(b)]2,3]. In this work, a simplified approach for predicting vapor-liquid equilibrium (VLE), B.P., and D.P. for non-ideal binary solutions that form azeotropes is developed.

When a non-ideal binary solution forms an azeotrope, the liquid-phase composition is identical to the vapor-phase composition (Xi,az= Yi, az, i= 1, 2) at the temperature of Taz. Basically, at the azeotropic condition, the two components have the same volatility. So, the boiling liquid produces vapor with the same composition as that in the liquid phase. By canceling Yi and Xi from both sides of Eqs. 1 and 2, the activity coefficients of the components at Xi,az can be easily calculated by Eqs. 3 and 4:

$\gamma _{1,az}=\frac{P_{T}}{P_{1}^{sat}(T_{az})}$ (3)

$\gamma _{2,az}=\frac{P_{T}}{P_{2}^{sat}(T_{az})}$ (4)

P sat, the vapor pressure of pure species i, can be calculated by the Antoine equation:

$1nP_{i}^{sat}(T)=A_{i}-\frac{B_{i}}{C_{i+T}}(i=1,2)$ (5)

where T= Taz. Once the γi, az’s at the azeotropic condition are calculated, we may substitute the γi, az values into empirical or theoretical models for computing model parameters. Three of the widely used empirical models that contain two parameters A12 and A21 for binary systems are tackled in this work [1(c)]:

Van Laar model

$1n\gamma _{1}=A_{12}\left ( \frac{A_{21}X_{2}}{A_{12}X_{1}+A_{21}X_{2}} \right )^{2}$ (6)

$1n\gamma _{2}=A_{21}\left ( \frac{A_{12}X_{1}}{A_{12}X_{1}+A_{21}X_{2}} \right )^{2}$ (7)

Margules model

$1n\gamma _{1}=[A_{12}+2(A_{21}-A_{12})X_{1}]X_{2}^{2}$ (8)

$1n\gamma _{2}=[A_{21}+2(A_{11}-A_{21})X_{2}]X_{1}^{2}$ (9)

Wilson model

$1n\gamma _{1}=-1n(X_{1}+A_{12}X_{2})+X_{2} \left ( \frac{A_{12}}{X_{1}+A_{12}X_{2}} -\frac{A_{21}}{X_{2}+A_{21}X_{1}}\right )$ (10)

$1n\gamma _{2}=-1n(X_{2}+A_{21}X_{1})+X_{1} \left ( \frac{A_{21}}{X_{2}+A_{21}X_{1}} -\frac{A_{12}}{X_{1}+A_{12}X_{2}}\right )$ (11)

RESULTS OF COMPUTATION FOR MODEL PARAMETERS

A binary system containing 1-propanol (species 1) and water (species 2) is chosen for illustrating the procedure developed in this work. Published azeotropic condition for this binary system at atmospheric pressure (PT = 1 atm or101.325 kPa) is listed in Table 1.

Table 1: Azeotropic condition for the binary mixture of 1-propanol (species 1) and water (species 2) at 1 atm [5].

Taza (°C)	X1,az ( = Y1,az ) by mole	X2, az( = Y2,az)
87.7	0.432	0.568

The parameters of the Antoine equation for computing the vapor pressure of pure components are listed in Table 2.

Table 2: Parameters of Antoine equation for the 1-propanol and water

(Appendix A, Ref.[14] ):

Ln[P (kPa)] = A – B/[ C + T (°C) ]

	A	B	C
1-propanol	16.1154	3483.67	205.807
water	16.3872	3887.70	230.170

By substituting the data from Tables 1 and 2 into Eqs. 3-5, we may obtain

$P_{1}^{sat}(T_{az})=69.8451kPa,\gamma _{1,az}=1.45071$ (12)

$P_{2}^{sat}(T_{az})=63.8623kPa,\gamma _{2,az}=1.58662$ (13)

When the γ1,az and γ2,az values from Eqs. 12 and 13 and azeotropic data from Table 1 are substituted into Eqs. 6 and 7 to compute the parameters for the Van Laar model, it is noted that the ratio A21 / A12 can be easily obtained by dividing Eq. 6 with Eq. 7:

$\frac{A_{21}}{A_{12}}=\frac{1n\gamma _{1,az}X_{1,az}^{2}}{1n\gamma _{2,az}X_{2,az}^{2}}=0.466237(VanLaar)$ (14)

Equation 14 is then plugged back into either Eq. 6 or 7 to solve for A12 and A21. Similarly, the values from Eqs. 12 and 13 and Table 1 are substituted into the Margules model (Eqs. 8 and 9) and the values of A12 and A21 may be obtained easily by solving the two linear algebraic equations simultaneously. As far as the Wilson model is concerned, a procedure using Excel’s solver is illustrated below. Initially, values of A12 and A21 are guessed. Then, the activity coefficients are predicted using Eqs. 10 and 11. The sum

of square of errors $[\left ( \gamma _{1,az}-\gamma{_{1,az}}^{pred}\right )^{2}+\left ( \gamma _{2,az}-\gamma{_{2,az}}^{pred} \right )^{2}]$

is set at the minimum value by changing the two guessed values of A12 and A21simultaneouslyusing Excel’s Solver tool. Table 3

Table 3: Solver procedure for finding Wilson model parameters. The target cell (sum of square of errors) is set at the minimum value by changing the cells containing the guessed A12 and A21 values simultaneously using Excel Solver. Guessed Values of A12 and A21 A12: 0.0210280 A21: 0.724013

γ1,az

(Eq. 3)

γ2,az (Eq.4)

γ pre (Eq. 10)

1,az

γ pre (Eq. 11)

2,az

(γ -γ pre)2

1,az 1,az

(γ -γ pre)2

2,az 2,az

Sum of square of errors

1.45071

1.58662

1.45071

1.58662

1.94054 x 10-13

8.35545 x 10-15

2.02409 x 10-13

shows the procedure and results of computation by Excel for the Wilson model parameters.

The results of computation for the parameters of all three models based on the published azeotropic condition (for the binary mixture of 1-propanol and water at 1 atm) are summarized in Table 4.

Table 4: Summary of Parameters of Van Laar, Margules, and Wilson models based on the azeotropic condition of the 1-propanol/water mixture at 1 atm.

	Van Laar	Margules	Wilson
A12	2.57597	2.29390	0.0210281
A21	1.20101	0.97366	0.7240130

VLE BP AND DP CALCULATIONS

Once the model parameters are obtained based on the azetropic condition of the binary system, we may assume that these parameters are weak functions of temperature and may still be valid for the whole range of B. P. encountered at various compositions under the desired system pressure PT . A procedure for calculating B. P. at any liquid-phase composition (X1 and X2 (= 1- X1 )) is outline below:

1) Guess the temperature T of the binary mixture.

2) Calculate the vapor pressures P1 sat and P2 sat of the pure liquids at the guessed T (Eq. 5 and Table 2).

3) Calculate the activity coefficients γ1 and γ2 at this liquidphase composition according to any of the models chosen (Eqs. 6 and 7; Eqs. 8 and 9; or Eqs. 10 and 11).

4) Calculate the predicted total vapor-phase pressure PT pred = P1 + P2 according to Eqs. 1 and 2.

5) Use Excel Solver to find the root of the target equation PT pred - PT = 0 by changing the guessed value of T. In this work, PT is set at 1 atm (101.325 kPa or 1.01325 bar).

6) Once the root ( T ) is found, the vapor-phase composition is calculated as Y1 = P1 / PT and Y2 = P2 / PT (or simply Y2 = 1- Y1 )

7) A plot of Y1 vs X1 gives the VLE equilibrium curve. By plotting T vs. X1 and T vs. Y1 , we may obtain the B. P. curve

and the D. P. curve, respectively.

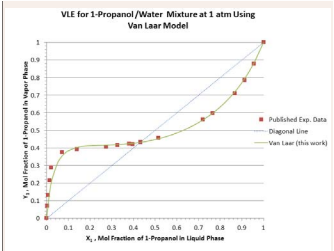
The results of computation for VLE data at 1 atm using Van Laar, Margules, and Wilson model parameters from the azetropic condition are presented in Figure 1.

Figure 1: Vapor-liquid equilibrium compositions predicted by the Van Laar model for 1-propanol/water mixture at 1 atm.

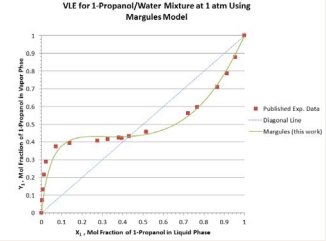
Figure 2.

Figure 2: Vapor-liquid equilibrium compositions predicted by the Margules model for 1-propanol/water mixture at 1 atm.

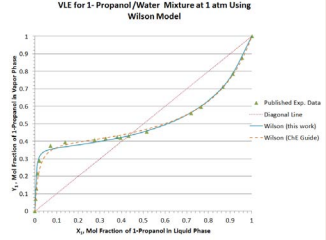
The predicted values are compared with the published experimental values available in the literature [4]. Excellent agreements exist between the predicted and the published VLE data. Moreover, using the spread sheet available in the website of ChE Guide [3], the results of prediction using Wilson model parameters based on the leastsquare regression over the whole ranges of temperature and liquid-phase composition at 1 atm are also plotted in Figure 3.

Figure 3: Vapor-liquid equilibrium compositions predicted by theWilson model for 1-propanol/water mixture at 1 atm.

It is evident that the simplified approach using Wilson model parameters from the azeotropic condition (this work) offers comparable quality of prediction as that based on the leastsquare regression over the whole ranges of temperature and composition.

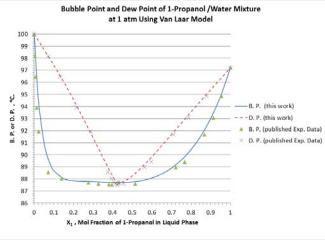
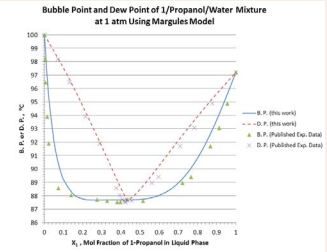
The results of computation for B.P. and D.P. using Van Laar, Margules, and Wilson model parameters from the azeotropic condition are presented in Figure 4.

Figure 4: P.and D. P. predicted by the Van Laar model for 1-propanol/ mixture at 1 atm.

Figure 4.

Figure 5: P.and D. P. predicted by the Margules model for 1-propanol/ mixture at 1 atm.

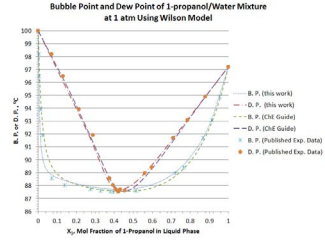
Again, using the spreadsheet provided by the website of ChE Guide [3], the results of computation using the Wilson model (based on the whole ranges of temperature and liquid composition under PT = 1atm) are also plotted in Figure 6.

Figure 6: P.and D. P. predicted by the Wilson model for 1-propanol/ mixture at 1 atm.

It is evident that the simplified procedure developed in this work offers excellent prediction of B. P. and D. P. at various liquid-phase compositions at 1 atm.

DISCUSSION

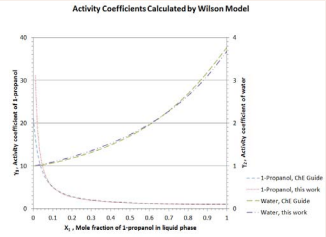
The simplified approach developed in this work mainly applies to non-ideal binary solutions that form azeotropes. Liquid-activity models containing two parameters are used in computing model parameters based on the azeotropic condition at 1 atm (or any other system pressure). When such model parameters are extended to compositions and B. P. away from the azeotropic condition, it is assumed in this work that model parameters are insensitive to changes in system temperature. In the literature, it has been reported that except at compositions near infinite dilution (X1 -->0), the activity coefficients for both components in the 1-propanol/water mixture vary insignificantly with temperature [5,6]. Rigorously speaking, parameters A12 and A21 of Van Laar, Margules, and Wilson models depend on temperature. As a matter of fact, mathematical expressions for Wilson model parameters as functions of temperature are available in the literature [1,2,6]. If the activity coefficients γ1 and γ2 using the Wilson model based on the simplified approach developed in this work are compared with those using the rigorous mathematical expressions (for temperature-dependent A12 and A21 in the Wilson model from ChE Guide [3]), it is found that the results agree very well (Figure 7).

Figure 7: Activity coefficients of 1-propanol and water calculated by Wilson model.

Major discrepancy between the two approaches only exists for 1-propanol near infinite dilution (X1 -->0). Evidently, there is only a very minor effect of temperature on the activity coefficients encountered in the binary system of 1-propanol/water at 1 atm [6].

In the literature, Van Laar constants for the 1-propanol/ water mixture at 760 mmHg (1 atm) by fitting the data collected over the whole range of composition to the model have been reported [5]. The best-fit A12 value from Ref. [5] is 2.6710 (after the original reported value of 1.160 is multiplied by ln (10) due to the different bases of logarithm used in Ref [5] and this work), which compares very well with the value 2.57597 obtained by the simplified approach developed in this work. Likewise, the best-fit A21 value from Ref. [5] is1.1582 (after the original reported value of 0.503 is multiplied by ln (10)), which agrees very well with the value 1.20101 obtained in this work.

The procedure developed in this work applies to miscible binary solution systems that are sufficiently non-ideal to form azeotropes. Also, one important limitation is that under a constant total pressure (resulting in varying B. P. as liquid-phase composition varies), the temperature has an insignificant effect on the parameters of the activity coefficient models determined from a single data point (namely the azetropic condition of the binary solution chosen). This can be true for non-ideal liquid mixtures that have very small heat of mixing [6] and whose B.P. varies in a small temperature range. For example, the rage of B.P. for the 1-propanol/water binary system is 87.7-100 °C under 1 atm. The parameters of activity coefficient models at any given composition would vary for only a few percent at different temperatures [5,6].

VLE for 1-propanol/water mixture at 1 atm is chosen in this work for illustration purpose. Interested readers may use the simplified procedure developed in this work to predict the VLE for any other binary systems whose azeotropic conditions under constant pressure (varying B. P. and D. P.) or constant temperature (varying total pressure) are known. This procedure is particularly suitable to undergraduate students or field engineers, who wish to understand fundamental concepts of liquid activity and make reasonable predictions of VLE based on limited information (i.e., azeotropic condition). However, important limitations (formation of azetropes, small heat of mixing, small B. P. range, and miscible liquid solution) mentioned above must be recognized for the constant pressure case. As far as the constant temperature case is concerned, model parameters determined from the azeotropic condition may extend more readily to liquid-phase compositions outside of the azeotropic composition. Exactly which empirical model fits a particular binary mixture better is beyond the scope of this work.

The thermodynamic behavior of mixed solution systems not only affects vapor equilibrium which is of vital importance in the design of separation processes, but also impacts the kinetics of many liquid-phase reactions and synthesis [7-10]. Information of VLE, particularly the compositions of azeotropes under different pressures [11] may be important in the operation of distillation columns that use pressure swing for separating binary mixtures [12,13].

CONCLUSION

The simplified procedure developed in this work allows the parameters of liquid activity models to be computed easily from the azeotropic condition of a non-ideal binary liquid solution. With the parameters of Van Laar, Margules, and Wilson models determined for the binary mixture, one may predict the equilibrium vapor-phase compositions, B.P. and D.P. at any other liquid-phase compositions under the assumption that model parameters are insensitive to temperature. Results of computations done in this work agree very well with published experimental data, as well as predictions made by more elaborate procedures in the literature.

REFERENCES

Smith JM, Ness HCV, Abbott MM. Intro to Chemical Engineering Thermodynamics. 5th edn. New York: Mcgraw-Hill College, 1996; (a) p. 449 ; (b) pp. 449-456 ; (c) pp. 386-388.
Shacham M, Brauner N. Solving a System of Nonlinear Algebraic Equations: You Only Get Error Messages--What to do Next?. Chem Eng Educ. Spring 2017; 51(2): 75-82.
Wilson – ChE Guide. 2017. https://cheguide.com/tag/wilson/
Dawe RA, Newsham DMT, Ng SB. Vapor-Liquid Equilibria in Mixtures of Water, n-Propanol, and n-Butanol. J Chem Eng Data. 1973; 18: 44- 49.
Murti PS, van Winkle M. Vapor-Liquid Equilibria for Binary Systems of Methanol, Ethyl Alcohol, 1-Propanol, and 2-Propanol with Ethyl Acetate and 1-Propanol-Water. Chem Eng Ser. 1958; 3: 72-81.
Perry RH, Chilton CH. Chemical engineers’ handbook. 5th edn. NewYork: McGraw-Hill, 1973. 13-8 to 13-10.
Khamparia S, Jaspal D. Adsorptive removal of Direct Red 81 dye from aqueous solution onto Argemone Mexicana. Sustain Environ Res. 2016; 26: 117-123.
Khamparia S, Jaspal DK. Evaluation of decoloration potential of Xanthium Strumarium seed hull for adsorption of Direct red 81 in aqueous solution. Environ Dev Sustain. 2016; 1-19.
Malhotra S, Jaspal DK. Kinetics of Enolisation of Acetophenone and p-Bromoacetophenone: Comparative Studies. Bull Chem React Eng Catal. 2013; 8: 105-109.
Malhotra S, Jaspal D. Kinetics of the Enolisation Reaction of m-Nitro Acetophenone Catalyzed by Amino Acids. Bull Chem React Eng Catal. 2014; 9: 16-22.
Wasylkiewicz SK, Kobylka LC, Castillo FJ. Pressure sensitivity analysis of azeotropes. Ind Eng Chem Res. 2003; 42: 207-213.
Knapp JP, Doherty MF. A new pressure-swing-distillation process for separating homogeneous azeotropic mixtures. Ind Eng Chem Res. 1992; 31: 346-357.
Abu-Eishah SI, Luyben WL. Design and control of a two-column azeotropic distillation system. Ind Eng Chem Process Des Dev. 1985; 132-140.
Poling BE, Prausnitz JM, Connell JPO. The Properties of Gases and Liquids. 5 edn. New York: McGraw-Hill Education, 2000.

Chemical Engineering and Process Techniques

Chemical Engineering and Process Techniques