Extraction of Ca(II) picrate (CaPic2) and SrPic2 with 18-crown-6 ether (18C6) and benzo-18C6 (B18C6) into 9 diluents were studied at T = 298 K. Their ion-pair extraction constants (Kex,ip = [MLPic2]org/[ML2+][Pic- ] 2 ) were determined at M = Ca, Sr, L = 18C6, and B18C6, where the subscript “org” refers to an org or a diluent phase. The plot of log Kex,ip vs. log KD,L based on the regular solution theory (RST) yielded a molar volume (cm3 /mol) ratio (V/VL) of MLPic2 against L as a slope and then the V values were evaluated. Here, KD,L = [L]org/[L] and its literature values and VL were employed. Also, apparent radii (r /Å) of the ion-pair complex, Pic-ML-Pic, in the phases were evaluated basically from the V values and the relation of V = 4πr 3 /3. Moreover, the log β2 values were obtained from intercepts of the RST plots only at the hydrophobic B18C6 systems: β2 =[M(B18C6) Pic2]/[MB18C62+][Pic- ] 2 . Additionally, the KD,MLPic2 (= [MLPic2]org/[MLPic2]) values for the 9 diluent/water systems were determined from the relation of KD,MLPic2 = Kex,ip/ β2. Using these values, the Ca(II) and Sr(II) extraction with L and forms for their MLPic2 complexes were characterized, compared with the CdPic2 and PbPic2 extraction with 18C6 and/or B18C6.

Alkaline-earth metal extraction; regular solution theory plots; molar volume; Overall ion-pair formation constants; Ca(II) and Sr(II) picrates; 18-crown-6 ether derivatives

Jin Q, Numako C, Kudo Y (2023) Regular-Solution-Theoretical Analysis of Ca(II) and Sr(II) Picrates Extraction with 18-Crown-6 Ether Derivatives into Various Diluents. Chem Eng Process Tech 8(1): 1072.

The regular solution theory (RST) has been applied for alkali metal {Li(I)-Cs(I)} picrates extraction with some crown ether compounds (L) into more than ten diluents [1]. From such studies, the following equation has been derived [1-4]:

log KD,MLAn = (V/VL)log KD,L + g

or

log Kex,ip = (V/VL)log KD,L + g + log βn                                  (1)

with Kex,ip = [MLAn]org/[MLn+ ][A- ]n = βnKD,MLAn, where the symbols, g, Mn+ and A- , denote a function containing a solutesolvent interaction term, a metal ion, and a counter anion, respectively, and the subscript “org” shows an organic or a diluent phase. Additionally, KD,MLAn refers to the distribution constant of an ion-pair complex, MLAn, between water (w) and the diluent phases and Kex,ip and βn do to an ion-pair extraction constant for MLAn and its ion-pair formation one in water (see below about n = 2), respectively. Also, V and VL denote molar volumes (cm3 /mol) of MLAn and the free L in a phase, respectively. Then, similar procedures have been applied to the extraction of Cd(II) and Pb(II) salts, such as chloride [5], bromide [3], iodide [6], and picrate (MPic2) [3,4,7,8], with L = 18-crown-6 ether (18C6) or its mono-benzo derivative (B18C6). These extraction experiments easily yield Kex,ip, not KD,MLA2. Therefore, the plot of log Kex,ip versus log KD,L at n = 2 has given V/VL as a slope and the g term with log β2 as an intercept. Here, the g term is a function of cohesive energy densities [1,2,9,10] and the constant β2, which is defined as [MLA2]/[ML2+][A- ]2 , satisfies the relation, Kex,ip = β2KD,MLA2 {see Eq. (1)}. So, size characters of Cd(18C6)A2 with A- = Cl- , Br- , I- , and Pic- and Pb(18C6)Pic2 were discussed using the V values and apparent radii estimated from them [10].

In the present paper, we studied the extraction of CaPic2 and SrPic2 with 18C6 and B18C6 into nine diluents at T = 298 K. Primarily, two extraction constants (Kex & Kex±), a distribution constant (KD,Pic) of Pic- into the org phases, a M2+ incorporative constant (KM/ML) with L into the org phase, and Kex,ip were determined with an estimation of ionic strength (I ) for the w phase. Here, the former four constants were defined as [MLPic2] org/P, [MLPic+ ]org[Pic- ]org/P with P = [M2+][L]org[Pic- ]2 , [Pic- ] org/[Pic- ], and [ML2+]org/[M2+][L]org, respectively. Then, from the above constants and so on, we derived the ionic strength, Iorg, for the org phases, overall ion-pair formation constants {β2,org =[MLPic2]org/[ML2+]org([Pic- ]org)2 } for the org phases, and the third extraction constants {Kex2± = [ML2+]org([Pic- ] org)2 /P} given for the ML2+ extraction. Moreover, the V and β2 values were determined from the RST plots with log Kex,ip and thereby sizes of MLPic2 in phases were discussed. Additionally,some extraction or distribution properties of the present Ca(II) and Sr(II) extraction systems with 18C6 and B18C6 were characterized in comparison with the Cd(II) and Pb(II) systems [3,4,7,8,10] reported before.

Chemicals

Purities of commercial Ca(NO3)2⋅4H2O {Kanto, guaranteedpure reagent (GR), 98.5%} and Sr(NO3)2 (Kanto, GR, 98.0%) were determined by the complexometric titration with Na2EDTA⋅2H2O (Dojindo, Japan, >99.5%). 18C6 {Extra pure reagent (EP), 98.0%} and B18C6 (EP, > 96.0%) were purchased from Tokyo Chemical Industries. These reagents were dried for more than 20 h under a reduced pressure. The purities of these L were checked by measuring their melting points. Found: 37.0- 37.5 or 36.5-37.5 °C for 18C6 and 42.2-43.1 or 42.7-43.3 for B18C6. A concentration of the aqueous solution of picric acid (Wako, GR, 99.5%; abbreviated as HPic) was determined by the acid- base titration with a standardized aqueous solution of NaOH (Kanto, GR. >97.0%).

The following organic solvents were used as diluents. Except for toluene (Wako, GR, 99.5%), other eight solvents of GR grade were purchased from Kanto Chemical Industries: benzene (99.5%); bromobenzene (98.0%); chlorobenzene (99.5%); chloroform (99.0%); 1,2-dichloroethene (99.5%); dichloromethane (99.5%); m-xylene (98.0%); o-dichlorobenzene (99.0%). All the solvents were washed three times with pure water and kept in bottles at condition saturated with pure water [11]. Other reagents used were of GR grade.

Abbreviations of the diluents used here were as follows: bromobenzene (BBz); benzene (Bz); chlorobenzene (CBz); chloroform (CF); 1,2-dichloroethene (DCE); dichloromethane (DCM); m- xylene (mX); o-dichlorobenzene (oDCBz); toluene (TE).

Extraction Experiments and their Data Analyses

Aqueous mixtures of [Ca(NO3)2]t = 0.0050 mol/L, [HPic]t = 0.010-0.012 mol/L, and [18C6]t = (0.25-7.1) × 10-3 or [B18C6] t = (0.35-4.7) × 10-3 mol/L were prepared, where [ ]t refers to a total concentration. Similarly, the mixtures of [Sr(NO3)2] t = 0.0050 mol/L, [HPic]t = 0.010-0.012, and [18C6]t = (0.076- 4.2) × 10-3 or [B18C6]t = (0.071-3.2) × 10-3 were prepared. Ten mL of these mixtures were mixed with the same volumes of the diluents in the stoppered glass tubes of about 30 mL and then shaken in a thermostated water bath for about 2 h at 298 K. Other experimental procedures, such as back extraction and centrifugation, were essentially the same as those reported before [3,7,11]. After the extraction, the pH values of separated w phases were measured: pH readings were in the ranges of 2.17- 2.38 for the Ca(II)-18C6 extraction system, 2.20-2.37 for Ca(II)- B18C6, 2.23-2.40 for Sr(II)-18C6, and 2.18-2.37 for Sr(II)-B18C6. About pH/ion meter and atomic absorption spectrophotometer, the same apparatus were used for the quantitative analyses of the phases [11,7,3].

An extraction model and details for data analyses were described in Appendix I. For the present systems, the experimental values of [L]t(max.)/[L]t(min.) for the plots against log Kexmix (see below) were in the ranges of 2.0 {for the Sr(II) extraction with L = B18C6 into Bz} to 18 {for the Ca(II) one with 18C6 into CBz} (see footnotes a & b of tables in Appendix II). 

About Composition of Extracted M(II) Species and Some Fundamental Equilibrium Constants for Extraction

Compositions of Ca(II) or Sr(II) : L were determined by using a common method [3-8,12]. Their values, namely the slopes of the log (D/[Pic- ]2 )-versus-log [L]org plots, were in the ranges of 0.92-1.05 at the correlation coefficient (R ) = 0.960-1.00 for the Ca(II)-18C6 system, 0.97-1.06 at R= 0.966-0.998 for Ca(II)- B18C6, 0.91-1.03 at R = 0.902-0.998 for Sr(II)-18C6, and 1.00- 1.08 at R = 0.922-0.995 for Sr(II)-B18C6. Here, the symbol D means an experimental distribution ratio of M(II) species about the diluent/water system and was calculated from the result of an AAS measurement. On the basis of these results, at least, we proved MLPic2 as one of extracted species into the diluents saturated with water.

Also, in order to determine some equilibrium constants, such as Kex and KD,Pic, −log ([M2+][L]org[Pic- ]) and –log P 1/2 were plotted against the logarithm of an extraction-constant parameter [3], log Kexmix. Here, the symbol Kexmix was defined as [AAS-analyzed total concentration of M(II) in the org phase]/P. So, this parameter was approximately expressed as

log Kexmix ≈ log {([MLPic2]org + [MLPic+ ]org)/P }= log {Kex + KD,Pic/([M2+][L]org[Pic- ])} = log {Kex + (Kex±/P)1/2}

(2) with [MLPic+ ]org ≈ [Pic- ]org or [MLPic+ ]org > 2[ML2+]org + [MPic+ ]org in the charge balance equation, 2[ML2+]org + [MLPic+ ] org + [MPic+ ]org = [Pic- ]org about the org phase. Moreover, the Kex,ip values were calculated from the relation of Kex,ip = KexKD,L/KML: KML = [ML2+]/[M2+][L] (see the footnotes d or e in Tables A1 to A2b about their values in Appendix II).

Additionally, the [ML2+]org values were estimated approximately from [ML2+]org = ([Pic- ]org − [MLPic+ ]org)/2 with [MLPic+ ]org ≈ [Pic- ](Kex±[M2+][L]org)1/2 with [MLPic+ ]org ≈ [Pic- ] org. Then, average KM/ML values were calculated only about the data of [ML2+]org > 0 (Tables A1 to A2b), where KM/ML = [ML2+] org/[M2+][L]org [13].

As can be seen from Tables A1 to A2b in Appendix II, the log Kex values obtained from the plots of log Kexmix versus −log ([M2+][L]org[Pic- ]) disagreed with those from the plots with –log P 1/2 at P = [M2+][L]org[A- ]2 . These cases were those of the Ca(II)- 18C6 extraction into DCE, oDCBz, DCM, CBz, BBz, and Bz, the Sr(II)-18C6 one into DCE and DCM, the Ca(II)-B18C6 extraction into DCE, BBz, and CF, and the Sr(II)-B18C6 one into BBz and CF: but the orders of their Kex were equal each other. These facts suggest difficulties on the data analyses for these diluent systems. In the following discussions, the Kex values of the former plots with −log ([M2+][L]org[Pic- ]) were basically adopted.

Several Equilibrium Constants Derived from Fundamental Constants

From the data in Tables A1 to A2b, we can easily derive the following equilibrium constants, using the thermodynamic cycles of the overall extraction and other equilibria [3-8,11,13].

log Kex2± = log {[ML2+]org([A- ]org)2 /P } = log KM/ML + 2log KD,A,                 (3)

log KD,ML = log ([ML2+]org/[ML2+]) = log KM/ML + log KD,L – log KML,            (4)

log K1,org = log ([MLA+ ]org/[ML2+]org[A- ]org) = log Kex± – log Kex2±,              (5)

log K2,org = log ([MLA2]org/[MLA+ ]org[A- ]org) = log Kex – log Kex±,                (6)

log β2,org = log K1,orgK2,org = log {[MLA2]org/[ML2+] org([A- ]org)2 } = log Kex – log Kex2±.     (7)

In these equilibrium constants, the log Kex2± and log β2, org values were evaluated, because the two values have been lessdiscussed so far. Such values are shown in Tables 1 and 2 with ionic strength values, I & Iorg, for w and org phases.

The log Kex2± values of 18C6 were larger than or close to those of B18C6 in many cases. The same trend is true of the log Kex values, except for the Sr(II)-18C6/B18C6 extraction into DCM (see Tables A2 & A2b in Appendix II). Also, the log Kex± values hold the same trend, except for the Ca(II)-18C6/B18C6 extraction into TE and mX (Tables A1 & A1b in Appendix II) and the Sr(II)- 18C6/B18C6 one into CF (Tables A2 & A2b). Consequently, it was shown that extraction-abilities of 18C6 are higher than those of B18C6 in many ML2+ extraction systems with M = Ca and Sr.

The log β2,org values were in the ranges of 8.8-13.7 for the Ca(II)-18C6 extraction system, 9.8-14 for Ca(II)-B18C6, 8.9-16 for Sr(II)-18C6, and 10.4-14 for Sr(II)-B18C6 (see Tables 1 & 2). While the values for the Cd(II) extraction systems have been reported to be in the ranges of 13.0-15 at B18C6 [8] and 16.1 into oDCBz and 14.9 into BBz at 18C6 [13]. These results suggest that the interaction between CdL2+ and Pic- at L = B18C6 (& 18C6) is comparatively stronger than that between CaL2+ or SrL2+ and Picin the diluents saturated with water (see the V values in Table 3).

Characterization of MLPic2 in Phases Based on Data of RST Plots

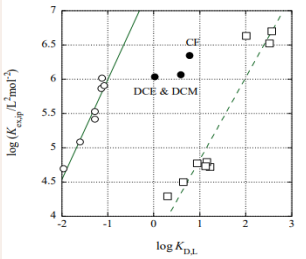
The log Kex,ip values were plotted against the log KD,L ones based on the RST for the present extraction systems. Generally, these plots are expressed with Eq. (1) [1-9]. Thus-obtained straight line was log Kex,ip = (1.46 ± 0.18)log KD,L + (7.46 ± 0.24) at R = 0.965 for the Ca(II)-18C6 system (see the circles in Figure 1)

Figure 1: RST plots for the Ca(II)-18C6 (open circles) and Sr(II)-B18C6 (squares) systems. The three points of the full circles were omitted from the calculation of the regression line for the 18C6 system.

without the extraction data at org = DCE, DCM, and CF. Others were slope =

1.6 ± 2.4 and intercept = 6.6 ± 3.0 at R = 0.312 for the Sr(II)- 18C6 system without the data at DCE, DCM, CF, and mX, 0.65 ± 0.14 and 6.05 ± 0.23 at R = 0.862 for Ca(II)-B18C6, and 1.20 ± 0.14 and 3.63± 0.22 at R = 0.954 for Sr(II)-B18C6 (see the squares in Figure 1). From the equations, the V values and apparent radii (r /Å) about Pic-ML-Pic were estimated essentially using V = (experimental slope)VL at L = 18C6 and B18C6 and V = 4r3 /3 [10], respectively.

Table 3 shows their values together with the sums, (r+ + r-) and (r+ + 2r-), of an effective ionic radius (r+/ Å) [14] of six-coordinated M2+ with a radius (r- = 3.35 Å [15]) of Pic- . Also, we can see simply that the larger errors on V in Table 3 reflect the larger deviations among the diluent systems. Moreover, the errors (δr) of r were calculated from the relation [16], δr = |dr/ dV |δV, with |dr/dV | = (3/4π)1/3V −2/3/3 = 0.2067V −2/3, where the symbol δV refers to the experimental error of V at Å3 /mol unit.

(i) About judging unsuitable data for the RST plot. About the above RST plots of the 18C6 systems, it was suggested that the three or four diluent molecules more-strongly interact with M(18C6)Pic2 [1]. The authors analyzed this suggestion as follows.

The process of Kex,ip is expressed with two thermodynamic processes at least. That is, a) ML2+ + 2A- ? MLA2 and MLA2? MLA2,org [5,8] and b) ML2+ + 2A- ? ML2+org + 2Aorg and ML2+org + 2Aorg ? MLA2,org. These equilibrium constants were expressed as β2, KD,MLA2, KD,ML-2A = KD,ML(KD,A)2 {= [ML2+] org[A- ]org2/([ML2+][A- ]2 )}, and β2,org, respectively. From Eq. (1), we obtained the following equations.

log Kex,ip = log KD,MLA2 + log β2 [5,8] = log KD,ML-2A + log β2,org = (V/VL)log KD,L + g + log β 2 (1a)

Obviously, in the process a), log KD,MLA2 is proportional to log KD,L [5,8], because the log β2 values are nearly constant for the I values shown in Table 1.

Table 1: Derived constantsa, Kex2± and β2,org, of CaPic2 extraction with L into various diluents and the I and Iorg values at T = 298 K.

Diluents	L = 18C6				B18C6
	I/mol L-1	Iorg/10-4 mol L-1	log Kex2±	log β2,org	I/mol L-1	Iorg/10-4 mol L-1	log Kex2±	log β2,org
DCE	0.019	2.5	-2.42 ±0.32	8.89 ±0.32	0.019	1.1	-4.21 ±0.38	10.18 ±0.38
oDCBz	0.020	0.90	-2.51 ±0.36	9.01 ±0.07	0.019	0.055	-7.9 ±1.6	14.3 ±1.6
DCM	0.014	2.5	-3.00 ±0.37	8.94 ±0.37	0.019	0.50	-5.30 ±0.48	10.81 ± 0.48
CBz	0.020	1.7	-1.68 ± 0.50	9.13 ± 0.50	0.019	0.23	-5.63 ± 0.72	12.13 ± 0.72
BBz	0.020	0.35	-3.65 ± 0.38	11.27 ± 0.38	0.019	1.2	-3.40 ± 0.49	9.86 ± 0.49
CF	0.021	2.1	-5.42 ± 0.64	11.45 ± 0.64	0.021	017	-6.50 ± 0.41	11.81 ± 0.41
Bz	0.019	1.6	-2.03 ± 0.45	9.19 ± 0.45	0.019	0.076	-6.97 ± 0.91	13.13 ± 0.91
TE	0.019	0.034	-6.56 ± 0.93	13.71 ± 0.93	0.019	0.27	-5.54 ± 0.37	11.67 ± 0.37
mX	0.019	0.080	-5.26 ± 0.52	12.38 ± 0.52	0.019	0.58	-4.74 ± 0.43	10.70 ± 0.44
aSee the text.

This fact indicates that The RST plots reflect the weak interaction of the neutral MLPic2 with the diluent molecules. Unfortunately, we cannot adopt this process, because of lack of the β2 and KD, MLA2 values in the present extraction model (see Appendix I). So, the log KD,ML-2A and log β2,org values were plotted against the log KD,L ones (see Figures 2 & 3), together with the log Kex,ip values.

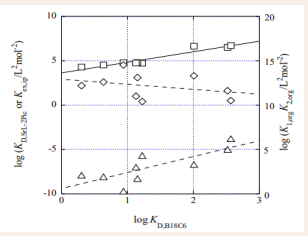
Figure 2

Figure 2: RST plot (squares) for the Sr(II)-B18C6 system and plots of log KD,SrL-2Pic (triangles) and log K1 ,orgK2 ,org (diamonds) vs. log KD,B18C6, where KD,SrL-2Pic = KD,SrL(KD,Pic)2 and K1,orgK2,org = β2,org. See the text for the regression lines.

shows that the log KD,SrL-2Pic values are fundamentally proportional to the log KD,B18C6 ones. The regression lines were log KD, SrL-2Pic = (1.81 ± 0.53)log KD, B18C6 + (-9.42 ± 0.84) at R = 0.792 and log β2,org = (-0.59 ± 0.62) log KD,B18C6 + (12.9 ± 1.0) at R = -0.340. A sum (= 1.2 ± 0.8) of these slopes is in good agreement with the slope (= 1.20) of the RST plot. Also, log KD, CaL-2Pic was equal to (0.92 ± 0.66) log KD, B18C6 + (-6.0 ± 1.0) at R = 0.466, although the R value was low. Additionally, log β2,org was (-0.27 ± 0.67)log KD,B18C6 + (12.0 ± 1.1) at R = -0.152 for Ca(II)-B18C6 system. Similarly, the sum (= 0.65 ± 0.94) equals the slope (= 0.65) of the RST plot. From these findings, we can see that the log KD, ML-2Pic values are mainly reflected into the positive slopes of the log Kex,ip versus log KD,L plots. In other words, the RST plots apparently depend on the total interaction of ML2+ and Pic- with the diluent molecules table 2.

Table 2: Derived constantsa, Kex2± and β2,org, of SrPic2 extraction with L into various diluents and the I and Iorg values at T = 298 K.

Diluents	L = 18C6				B18C6
	I/mol L-1	Iorg/10-5 mol L-1	log Kex2±	log β2,org	I/mol L-1	Iorg/10-5 mol L-1	log Kex2±	log β2,org
DCE	0.019	2.1	-4.64 ± 0.45	11.92 ± 0.45	0.019	0.56	-6.29 ± 0.57	13.32 ± 0.57
oDCBz	0.019	0.67	-3.04 ± 0.62	12.52 ± 0.62	0.020	5.6	-4.49 ± 0.58	10.40 ± 0.58
DCM	0.019	3.7	-4.45 ± 0.49	10.87 ± 0.49	0.019	1.6	-5.15 ± 0.47	11.56 ± 0.48
CBz	0.019	2.3	-4.41 ± 0.83	11.92 ± 0.84	0.019	0.87	-7.0 ± 1.1	13.1 ± 1.1
BBz	0.019	1.7	-0.13 ± 0.50	8.96 ± 0.58	0.019	3.5	-5.01 ± 0.47	11.02 ± 0.47
CF	0.020	2.1	-5.06 ± 0.71	11.85 ± 0.71	0.020	4.1	-3.92 ± 0.59	10.46 ± 0.60
Bz	0.019	5.3b	-3.42 ± 0.53	11.26 ± 0.53	0.019	0.23	-8.2 ± 2.0	14.5 ± 2.0
TE	0.019	0.69	-8.7 ± 4.3	16.8 ± 4.3	0.019	1.4	-6.31 ± 0.64	12.58 ± 0.64
mX	0.018	4.3	-1.4 ± 1.0	11.5 ± 1.1	0.018	1.7	-5.84 ± 0.77	12.23 ± 0.77
aSee the text. bCharge-balance condition of [Pic-]org > [ML2+]org was not satisfied on the successive approximation.

Considering the positive effect of log KD,ML-2Pic on the RST plots, the data at org = DCE, DCM, and CF seem to give its negative effect on the plot with log KD,ML-2Pic for the Ca(II)-18C6 system (see Figure 3).

Figure 3: Plots of the experimental r vs. (r+ + r-) for MLPic2 at M = Ca, Sr, with L = 18C6 (open circles) and B18C6 (open squares), for Cd(18C6)X2 (full circles) with X = Cl, Br, and I and M(18C5)Pic2 (full circles) at M = Cd and Pb, and for Cd(B18C6)Pic2 (full square). See Ref. [10] about the data of the full circles and square. The dotted line is r = (r+ + r-).

Additionally, the positive effect of log β2,org on the plot cannot cancel out the effect of log KD,CaL-2Pic with the three diluents. So, judging that the interaction with the three diluents is different to that based on RST, we omitted the three data from the RST plot for the Ca(II)-18C6 system. The thus-obtained line was log KD, CaL-2Pic = (4.9 ± 1.3)log KD,18C6 + (1.4 ± 1.8) at R = 0.880. The same judging was applied for the Sr(II)-18C6 system: the lines were log KD,SrL-2Pic = (11.4 ± 3.4)log KD,18C6

+ (5.8 ± 4.3) at R = 0.887 and log β2, org = (-11.1 ± 4.5) log 

KD,18C6 + (-1.4 ± 5.6) at R = -0.821 without org = DCE, DCM, CF, and mX. However, we did not add this Sr(II) system to the following detailed discussions, because its R value of the RST plot was very low.

(ii) About V. Being different from the result of CdLPic2 [10], increases in V due to the benzo group were not observed among MLPic2 at M = Ca and Sr. For a given M2+, ion pairs with 18C6 were larger than or equal to those with B18C6. Namely, the bulkiness, V18C6 ≤ VB18C6, of L are not necessarily reflected to the present ion-pair’s V.

While, according to our previous paper [10], the V values have been 171 cm3 /mol (Table 3)

Table 3: Molar volumes (V ) and apparent radii (r ) of MLPic2 in phases at M = Cd, Pb, Ca, and Sr and T = 298 K.

MLPic2	V a /cm3 mol-1	r b/Å	(r+ + r-)c/Å	a b/degree	(r+ + 2r-) cos a/Å	(r+ + 2r-)d /Å
Cd(18C6)Pic2	171e	4.1e	4.30e	32	6.4	7.65
Ca(18C6)Pic2	312±78	5.0±0.4	4.35 (=	40 {= sin-	5.9 (= 7.70	7.7
			1.00 + 3.35)	1(5.0/7.70)}	cos 40°)
Sr(18C6)Pic2	330±512	5.1±2.6	---f	---f	---f	7.88
Pb(18C6)Pic2	205e	4.3e	4.54e	33	6.6	7.89
Ca(B18C6)Pic2	164±41	4.0±0.3	4.35	31	6.6 at a = 31°	7.7
Sr(B18C6)Pic2	301±49	4.9±0.3	4.53	38	6.2 at 38°	7.88
18C6 without MPic2g	214±47	4.4±0.3	1.34-1.48h,	---f	---f	---f
B18C6 without MPic2g	252±28	4.6±0.2
a Determined from the slopes of the RST plots. b Values estimated from a postulated relation of V = 4r 3/3 and assumed to be (r+ + 2r-)sin. c Sum of effective ionic radius (r+) of six-coordinated M2+ with the radius (r- = 3.35 Å) of Pic- .   It satisfies the condition of = 90. See Refs. [14] & [15]. d Abbreviated as Rbulk = r+ + 2r-. e Ref. [10]. f Not calculated. g Ref. [1].  h Cavity size of L. See Refs. [17].

for Cd(18C6)Pic2 and 249 for Cd(B18C6)Pic2. Also, the V values of SrLPic2 seem to be larger than those of CaLPic2 for a given L. These facts indicate that the V values of SrLPic2 and CaLPic2 depend on sizes of the central M2+. Similarly, it has been reported that the V value of Pb(18C6)Pic2 is larger than that of Cd(18C6)Pic2 (see above & Table 3). Here, the effective ionic radius of the six- coordinated Pb2+ with the electron configuration of [Xe](5d)10(6s)2 is 1.19 Å [14],whereas that of Cd2+ with [Kr](4d)10 is 0.95 [14]. So, we obtained M = Cd < Pb < Ca ≤ Sr (see Table 3) as the V order of M(18C6)Pic2. This order suggests that [Ca18C6]2+ and [Sr18C6]2+ have more bulky forms than [Pb18C6]2+ (& [Cd18C6]2+), considering the r+ order (Cd2+ < Ca2+ < Sr2+ < Pb2+).

(iii) About r. Table 3 shows the trend that the r values are larger than the (r+ + r-) ones, except for Ca(B18C6)Pic2 {, Cd(18C6)Pic2, & Pb(18C6)Pic2}. Here, we assumed that Pic-MLPic is close to a sphere and its radius r estimated corresponds to the center-to-center (CTC) distance or an apparent bond length in the interaction between M2+ included in L and Pic- . These results indicate the possibility that Ca(18C6)Pic2, Sr(18C6) Pic2, and Sr(B18C6)Pic2 are solvent-shared forms in the phases.

For the former two M(18C6)Pic2, effects of bulky [M(18C6)]2+ forms, based on the more- flexible 18C6 skeleton, are supposed additionally: see the above discussion (ii). Comparatively, it is suggested that Ca(B18C6)Pic2 in the phases is a contact ion-pair, such as Cd(18C6)Pic2 and Pb(18C6)Pic2 [10]. These three r values satisfy the condition of r ≤ (r+ + r-): see the open square and full circles below the straight line in Figure 4.

Figure 4: Plots of the experimental r vs. (r+ + r-) for MLPic2 at M = Ca, Sr, with L = 18C6 (open circles) and B18C6 (open squares), for Cd(18C6)X2 (full circles) with X = Cl, Br, and I and M(18C5)Pic2 (full circles) at M = Cd and Pb, and for Cd(B18C6)Pic2 (full square). See Ref. [10] about the data of the full circles and square. The dotted line is r = (r+ + r-).

(iv) About another consideration for r. Using the uncertain r- value of planar Pic- , it may be difficult to exactly discuss the structures of the MLA2 complexes predicted in the phases. Therefore, we propose another procedure for the r consideration as Appendix III. If the Pic-ML-Pic complexes are a compact form and the angle (α or ∠Pic-M-L) between the L-cavity plane including M(II) and the benzene-ring plane of Pic- is not 90°, then we can express the r values as (r+ + 2r-)sinα or (r+ + 2r-) cos α (see Appendix III). Here, the parameter (r+ + 2r-) reflects a bulkiness of the LM-Pic skeleton (see Table 3 for their values).

So, the angle α or ∠Pic-M-L can be estimated in the range of 0° to 90°. For example, the α value in the Pic-Ca18C6-Pic was obtained from 5.0 = 7.70sin α to be 40°. Similarly, the other α values were 31° {= sin-1(4.0/7.70)} for Pic-CaB18C6-Pic and 38° for Pic-SrB18C6-Pic (see Table 3). These results suggest that PicCaB18C6-Pic has a little more compact form than the other two complexes. This suggestion is not in conflict with the results {see (iii)} for the CTC distance, (r+ + r-). Similarly, the (r+ + 2r-)cos α values were estimated and summarized in Table 3.

For all MLPic2, the parameters, 100r/Rbulk with Rbulk = r+ + 2r-, were calculated. They were 53% for Cd-18C6, 65 for Ca18C6, 54 for Pb-18C6, 52 for Ca-B18C6, and 62 for Sr-B18C6. On the other hand, the 100r/Rbulk values of Cd(18C6)X2 were about 118% for X = Cl, 94 for Br, and 75 for I (from the data of Table A3 in Appendix III). In comparison with the r values of MLPic2, the values of Cd(18C6)X2 seem to reflect the bulkness distances of Cd-X. Thus, the results for 100r/Rbulk (< 70%) and α < 45° indicate that the Bz plane of Pic- slopes to the apparent L-cavity plane including M2+ or there are other interactions without the direct M2+-O− -C6H2(NO2)3 bonding. That is, the L-cavity plane does not vertically intersect to the Bz one, where both the hydroxyl oxygen atom and the Bz plane exist on the same plane.

For given α, the following orders about MLPic2 were obtained from Table 3.

Cd(18C6)Pic2: r < (r+ + r-) < Rbulkcos α < Rbulk;

Ca(18C6)Pic2: (r+ + r-) < r

Pb(18C6)Pic2: r < (r+ + r-) < Rbulkcos α < Rbulk and

Ca(B18C6)Pic2: r ≤ (r+ + r-) < Rbulkcos α < Rbulk;

Sr(B18C6)Pic2: (r+ + r-) < r < Rbulkcos α < Rbulk with r = Rbulksin α.

Recognizing that Cd(18C6)Pic2 and Pb(18C6)Pic2 are contact ion-pairs as well as the previous work [10], we can judge Ca(B18C6)Pic2 to be a similar contact-form. Accordingly, the other MLPic2 can be determined to be the solvent-shared (or water- shared) ion-pairs. Under the condition of α < 45°, the relation of r ≤ (r+ + r-) means the contact form about MLA2, while that of r > (r+ + r-) does the other form. Also, the relations of r ≤ Rbulkcos α were satisfied with all the MLPic2 complexes, where we call Rbulkcos α “a conditional bulkiness”, since this parameter depends on an extent of α. Additionally, the same was true of Cd(B18C6)Pic2: r = 4.6 Å [10], α = 37° {= sin-1(4.6/7.65)}, and Rbulkcos α (= 7.65cos 37°) = 6.1 Å. Thus, the above results that only the r values are observed experimentally suggest that the values of the conditional bulkiness, are virtually cancelled out by the bulkiness of L. As can be seen from Table 3, the conditional values of Rbulkcos α at Rbulk = r+ + 2r- are in the range of 5.9 to 6.6 Å, whereas the apparent diameter of L is about 9 Å.

From the above results, we obtained the relation of (r+ + r-) ≈ r (= Rbulksin α) Rbulkcos α

(iv) About a flow for presuming the forms of MLA2. The authors propose the following flow, from (1) to (3), for presuming the forms of MLA2 in phases. (1) Which conditions does the experimental r value satisfy better, r ≤ (r+ + r-) or r > (r+ + r-)? If r ≤ (r+ + r-) (see Figure 4), then the relation suggests a contact form as MLA2. If r > (r+ + r-) (see Figure 4), then the relation suggests another form, such as the solvent-shared ion-pair. (2) If 100r/Rbulk < 70% is satisfied, the A- anion cannot vertically intersect to the L-cavity plane including M2+. (3) Using either r = Rbulksin α or Rbulkcos α, we can evaluate the extent of α. In particular, the terms (2) and (3) can depend on strongly the form of the A- anion, such as spherical, linear, or planar form. Also, the term (1) presumes kinds of ion pairs.

Estimation of Overall Ion-pair Formation Constants of MLPic2 in Water Phase and Their Distribution Constants for Hydrophobic B18C6

According to the RST plots of log Kex,ip versus log KD,L for the MPic (M = Li-K) extraction with the hydrophobic B18C6 and benzo-15-crown-5 ether into the diluents, their intercepts of Eq. (1) equal the log β1 = log K1 (= log [MLPic]/[ML+ ][Pic- ]) values as first approximations [9]. Here, the g values have been practically close to zero in Eq. (1) for L = B18C6: their values were −0.68 for the NaPic-B18C6 system and +0.12 for KPic-B18C6 [9]. However, for the CdPic2-B18C6 extraction system, its g value has been reported to be −4.4 [8]. This difference may be due to that between MI (B18C6)Pic and Cd(B18C6)Pic2 in the interaction with H2O.

It is well known that the hydration (or de-hydration) phenomena are important for the distribution of L and MLn+ (n = 1, 2) into some diluents [18,19]. Also, the g value includes the terms based on the interaction between H2O (or a diluent molecule) and L or MLAn [1]. So, although the number of data is few, we tried to plotting the correlation between these g values and the Gibbs’ free energies (ΔGh0/kJ mol-1) of the hydration to Na+ , K+ , and Cd2+: their ΔGh0 values were -410, -337, and -1799 kJ mol-1, respectively [20]. Its straight line was g = 0.0029ΔGh0 + 0.81 at R = 0.993. Using this equation and the ΔGh0 data [20] for Ca2+ (-1592 kJ mol-1) and Sr2+ (-1446), their g values were estimated to be -3.8 and -3.4, respectively. From Eq. (1), we obtained the relation of (intercept of the RST plot) = 6.1 = -3.8 + log β2 for Ca(II) system and then did log β2 = 9.9. Similarly the value for the Sr(II) system was 7.0. These 1st-approximate values, determined at an average I, were shown in Table 4. 

Table 4: 1st-approximate log β2 and log KD, MLPic2 valuesa for various water/diluent systems at L = B18C6 and T = 298 K.

Diluents	M = Ca		Sr		Cdb
	log β2	log KD,MLPic2	log β2	log KD,MLPic2	log KD,MLPic2
DCE	9.9 at I = 0.019c mol/L	-2.3	7.0 at I = 0.019c mol/L	-0.4	-2.64
oDCBz		-2.7		-2.3	-3.22
DCM		-2.3		-2.5	-2.21
CBz		-2.7		--2.2	-2.69
BBz		-2.7		-2.3	-3.12
CF		-2.5		-0.3	-2.71
Bz		-3.2		-2.3	-3.56
TE		-3.6		-2.5	-3.08
mX		-4.1		-2.7	-3.53
aValues calculated from the relation of log KD,MLA2 = log Kex,ip – log β2, where β2 = [MLA2]/[ML2+][A-]2. bRef. [8]. cAverage ionic strength for the w phases. See Tables 1 & 2.

Also, the log KD, MLPic2 values were calculated from the relation, log Kex,ip = log (β2KD,MLPic2) and are summarized in Table 4.

Practically in order to determine the more-precise β2 value, we must include this ion-pair formation equilibrium into the extraction model, derive other analytic equations, such as Eqs. (A1) to (A3) in Appendix I, and then re-analyze the extraction data of the 9 diluents, using their equations. With the thus-obtained data, the next Kex,ip values are determined. Accordingly, the RST plot is performed for determining a new β2 value. Also we analyze the extraction data again. These operations are repeated until the β2 value becomes constant. Here, the authors discuss about the 1st- approximate values, because such operations are considered to be another study.

The 1st-approximate log KD,CaLPic2 values at L = B18C6 were in the order of mX < TE < Bz < oDCBz, CBz, BBz < CF < DCE, DCM. Also, the log KD, SrLPic2 ones were in that of mX < TE < Bz, oDCBz, BBz ≤ CBz << DCM < DCE < CF. On the other hand, the log KD, CdLPic2 values were in the order of dibutyl ether (-5.7) << Bz < mX < oDCBz < BBz < TE < CF < CBz < DCE < DCM [8]. The order of CaLPic2 is very close to that of SrLPic2 at L = B18C6, while that of CdLPic2 is partially different from their orders, especially in the positions of the TE and CBz systems underlined. Totally, we can see that the log KD, MLPic2 values of the chloro-alkanes are larger than those of the Bz derivatives. Using log β2 = 7.36 [21] at I → 0 for Cd(B18C6)Pic2 in water and the Davies equation [22], the log β2 value was estimated to be = 7.19 at I = 0.019 mol/L and T = 298 K. Here, this I value is average one of the present extraction systems with B18C6 (see Tables 1 & 2). Considering the experimental error (±0.2) of the RST plots, the 1st-approximate log β2(M) values at I = 0.019 mol/L were predicted to be in the order M = Sr ≤ Cd << Ca. Also, the sequence, KD, CdLPic2 ≤ KD,CaLPic2 < KD,SrLPic2, at L = B18C6 was observed. Consequently, the authors suppose that the experimental Kex,ip order of Cd < Sr < Ca comes from both the larger β2(Ca) and the 2nd-larger KD,CaLPic2 values. Here, the log Kex,ip values of Cd(B18C6)Pic2 at I = 0.02-0.095 mol/L have been reported to be 4.37 into DCE, 3.73 into oDCBz, 4.74 into DCM, 4.15 into CBz, 3.78 into BBz, 4.15 into CF, 3.19 into Bz, 3.76 into TE, and 3.43 into mX [8].

In many cases, the extraction abilities, evaluated from Kex2±, Kex, and Kex±, of 18C6 in the extraction with CaPic2 and SrPic2 were larger than those of B18C6. The β2,org values were in the lower ranges than in the β2,org range of the CdPic2 extraction with B18C6 (or 18C6). As similar to the distribution of Cd(B18C6) Pic2, the KD,M(B18C6)Pic2 values of the chloro-alkanes at M = Ca and Sr are larger than those of the Bz derivatives. The log β2(M) values at I = 0.019 mol/L were predicted to be in the order of M = Sr ≤ Cd << Ca. From the relation of log (Kex,ip/β2) = log KD,M(B18C6)Pic2, the log KD,M(B18C6)Pic2 order of M = Cd ≤ Ca < Sr was obtained tentatively.The results of the RST plots indicate that the real r values of Pic-ML-Pic essentially distribute between (r+ + r-) and (r+ + 2r-)cos α, namely between the CTC distance and the conditional bulkiness one in LM-Pic. At least, from the experimental r values, we were able to see that the ion-pair complexes with ∠Pic-M-L < 45 are majority in the phases. The authors proposed the flow, from (1) to (3), for presuming the forms of MLA2 in phases. Here, it shows at least that the relation of r with (r+ + r-) and the 100r/Rbulk value are key parameters. Using any measurements or procedures, of course, it will be necessary to experimentally check the results obtained from the flow. 

The authors thank Professor Shoichi Katsuta for his usage permission of the atomic absorption spectrophotometer (Hitachi, type Z-8200) and for his supporting to experiments with its spectrophotometer.

1. Takeda Y. Extraction of alkali metal picrate with 18-crown-6, benzo- 18-crown-6, and dibenzo- 18-crown-6 into various organic solvents. Elucidation of fundamental equilibria governing extraction-ability and -selectivity. Bunseki Kagaku. 2002; 51: 515-525.
2. Kudo Y, Fujiwara R, Katsuta S, Takeda Y. Hydration effect on the ion- pair extraction of lithium picrate by hydrophobic benzo-15-crown-5 ether into various less-polar diluents. Anal Sci. 2007; 23: 1003-1005.
3. Kudo Y, Horiuchi N, Katsuta S, Takeda Y. Extraction of cadmium bromide and picrate by 18-crown-6 ether into various less-polar diluents: Analysis of overall extraction equilibria based on their component equilibria with formation of their ion pairs in water. J Mol Liquids 2013; 177: 257-266.
4. Kudo Y, Takahashi Y, Numako C, Katsuta S. Extraction of lead picrate by 18-crown-6 ether into various diluents: Examples of sub-analysis of overall extraction equilibrium based on component equilibria. J Mol Liquids. 2014; 194: 121-129.
5. Kudo Y, Tomokata S. Extraction of cadmium chloride by 18-crown-6 ether into various diluents: A comparative study with bromide and picrate extraction systems. J Mol Liquids. 2018; 249: 904-911.
6. Kudo Y, Ishikawa Y, Ichikawa H. CdI2 extraction with 18-crown-6 ether into various diluents: Classification of extracted Cd(II) complex ions based on the HSAB principle. Amer. J Anal Chem. 2018; 9: 560- 579.
7. Kudo Y, Katsuta S, Ohsawa Y, Nozaki K. Solvent extraction of cadmium picrate by 18-crown-6 ether into several less-polar diluents and nitrobenzene: Re-evaluation of corresponding overall extraction systems. J Thermodyn Catal. 2015; 6: 6.
8. Kudo Y, Tanaka Y, Ichikawa H, Katsuta S. Determination of some component equilibrium- constants by Cd(II) picrate extraction with benzo-18-crown-6 ether into various diluents and their evaluation. J Anal Bioanal Tech. 2017; 8: 7.
9. Kudo Y, Usami J, Katsuta S, Takeda Y. On the difference between ion- pair formation constants of crown ether-complex ions with picrate ion in water determined by solvent extraction and by potentiometry. J Mol Liquids. 2006; 123: 29-37.
10. Kudo Y. Application of Molar Volumes Obtained From a Solvent

    Extraction Method for Estimation of Sizes of Metal Complexes with

    Crown Ethers in Phases. Inter J Chem. 2019; 11: 8.

11. Jin Q, Kudo Y. Extraction of Cd(II) picrate with benzo-18-crown-6 ether into benzene under the presence of nitric acide in water phases. Anal Sci. 2022; 25: 9.
12. Takeda Y, Kat? H. The solvent extraction of bivalent metal picrates by 15-crown-5, 18-crown-6, and dibenzo-18-crown-6. Bull Chem Soc Jpn. 1979; 52: 1027-1030.
13. Kudo Y. An approximation method for determining key extraction constants in the equilibrium- analysis of Cd(II) extraction with 18-crown-6 ether into some diluents. J Anal Pharm Res. 2017; 5: 5.
14. Shannon RD. Revised   crystal   ionic   radii   and   systematic   study of interatomic distances in halides and chalcogenides. Acta Crystallographica. 1976; A32: 751-767.
15. Katsuta S, Wakahayashi H, Tamaru M, Kudo Y, Takeda Y. Tetraalkylammonium picrates in the dichloromethane-water system; Ion-pair formation and liquid-liquid distribution of free ions and ion pairs. J Solution Chem. 2007; 36: 531-547.
16. Taylor JR (translated by S Hayashi, R Baba). An Introduction to Error Analysis: A Study of Uncertainties in Physical Measurements. 2nd ed., Tokyo Kagaku-Dojin, Tokyo. 2000; 68 (in Japanese).
17. Lamb JD, Izatt RM, Christensen JJ. Stability Constants of Cation- macrocyclic Complexes and Thei Effect on Facilitated Membrane Transport Rates in Progress in Macrocyclic Chemistry. ed. by RM Izatt, JJ Christensen, Vol. 2, Jhon Wiley & Sons, New York, Chichester, Brisbane, Tronto. 1981; 54.
18. Iwachido T, Minami M, Kimura M, Sadakane A, Kawasaki M, Tôei K. The coextraction of water into nitrobenzene with alkali and alkaline earth metal salts of 2,2’,4,4’,6,6’- hexanitrodipicrylamine in the presence of several crown ethers and cryptands. Bul Chem Soc Jpn. 1980; 53: 703-708.
19. Kikuchi Y, Sakamoto Y, Sawada K. Partition of alkali-metal ion and complex formation with poly(oxyethylene) derivatives in 1,2-dichloroethane. J Chem Faraday Trans. 1998; 94: 105-109.
20. Ohtaki H, Tanaka M, Funahashi S. Y?eki-hann? no Kagaku (Chemistry of Reactions in Solutions). Gakkai Shyuppan Center, Tokyo. 1980; 214- 215.
21. Kudo Y, Kobayashi Y, Katsuta S, Takeda Y. Ion-pair formation of cadmium-18-crown-6 ether complex ions with picrate and chloride ions in water and distribution of its picrate ion-pair complex into benzene. J Mol Liquids. 2009; 146: 60-65.
22. R de Levie. Aqueous Acid-Base Equilibria and Titrations in Oxford Chemistry Primers 80. ed. by RG Compton, Oxford University Press. 1999; 62.
23. Høiland H, Ringseth JA, Brun TS. Cation-Crown Ether Complex Formation in Water. II. Alkali and Alkaline Earth Cations and 12-Crown-4, 15-Crown-5, and 18-Crown-6. J Solution Chem. 1979; 8: 779-792.
24. Kudo Y, Takahashi Y, Katsuta S, Takeda Y. Extraction of several divalent metal picrates by 18-crown-6 ether derivatives into benzene: A refinements for analyzing extraction equilibria. Inter J Chem. 2013; 5: 90-102.
25. Takeda Y, Nishida M. Solvent extraction of various metal picrates with benzo-18-crown-6 into CHCl3. Bull Chem Soc Jpn. 1989; 62: 1468- 1471.