Purpose: In rare diseases, small sample sizes and high intrapopulation variability often produce insufficient statistical power, necessitating alternative analytical approaches that can efficiently interpret limited data.

Methods: A Bayesian framework, which combined both prior knowledge from a Phase 2 trial and observed data from a Phase 3 trial prematurely terminated for futility, was developed to assess the likelihood of achieving clinically meaningful treatment effects with ARRY-371797.

Results: The Bayesian reanalysis yielded a posterior Hazard Ratio (HR) of 0.54, indicating a possible 46% reduction in the risk of worsening heart failure or all-cause mortality compared to control. The probability that ARRY-371797 has any efficacy (HR < 1) was 93.75%. The interpretation of treatment efficacy was modestly impacted by the HR thresholds, with 89.89% probability of achieving at least a 10% reduction in the HR (moderate efficacy) and 83.82% probability of achieving a 20% reduction (high efficacy). In the sensitivity analyses, the probability of any efficacy was between 75.68% (non-informative prior) and 85.48% (optimistic prior).

Conclusions: By integrating prior knowledge, the Bayesian reanalysis overcame some of the limitations of a frequentist approach and uncovered potential efficacy signals that were previously obscured. A Bayesian framework should be considered more frequently in rare disease research, where traditional statistical methods often fail to fully capture the potential efficacy of novel treatments.

• Bayesian analysis; Rare diseases; Statistical methods.

Perrault L, LeLorier J (2025) From futility to understanding: Bayesian insights from a terminated rare disease trial. Int J Rare Dis Orph Drugs 7(1): 1020.

HR: Hazard Ratio

Rare diseases are conditions that affect a small proportion of the population, typically defined as fewer than 200,000 individuals in the United States [1], or fewer than 1 in 2,000 people in the European Union [2]. Despite their individual rarity, rare diseases collectively impact millions of people worldwide.

One of the major challenges in studying rare diseases is the scarcity of available data, which makes conducting clinical trials and interpreting their results especially difficult [3]. Small sample sizes and high variability within the patient population [3], often lead to insufficient statistical power, making it harder to detect meaningful treatment effects using conventional methods [4]. These issues underscore the need for alternative analytical approaches that can increase our understanding of the uncertainty and make the most of limited data.

The goal of this reanalysis was to demonstrate how a Bayesian framework can be used to reinterpret the results of a clinical study that was prematurely terminated due to futility. By applying Bayesian methods to data from the Phase 3 trial of ARRY-371797 in lamin A/C gene (LMNA)− related Dilated Cardiomyopathy (DCM) [5], we aimed to uncover potential treatment effects or meaningful insights that were not evident in the original frequentist analysis. This study sought to highlight the advantages of Bayesian approaches in rare disease research, particularly in making more efficient use of limited and uncertain trial data.

Design

This study presents a Bayesian reanalysis integrating prior information from a Phase 2 clinical trial [6], and an interim analysis of a prematurely terminated Phase 3 trial [5], both investigating a novel therapeutic intervention (the selective protein kinase inhibitor ARRY 371797) for LMNA-related DCM, a rare disease that frequently results in early mortality due to sudden cardiac death [7]. The aim was to update the estimate of the Hazard Ratio (HR) for the composite outcome in patients with LMNA-related DCM treated with ARRY-371797 and to assess the probability of achieving specific efficacy thresholds.

Data Sources

The Phase 2 trial was a single-arm study involving 12 patients with LMNA-related DCM, on background heart failure treatment, who received ARRY-371797 [6]. At week 12, patients had statistically significant increases from baseline in functional capacity, as well as lower concentrations of a cardiac biomarker [6].

The Phase 3 trial was a randomized, double-blind, placebo-controlled study. The trial was terminated after a planned interim analysis suggested futility, with no significant differences (p > 0.05) between groups at week 24 for all outcomes. The reported HR for the composite outcome of worsening heart failure or all-cause mortality was 0.43 (95% confidence interval [CI], 0.11 to 1.74; p = 0.23) [5].

Statistical Analysis

A Bayesian approach was used to combine the likelihood derived from the observed Phase 3 data with prior knowledge from the Phase 2 trial to gain insight into a potential treatment benefit, including the probability of achieving various levels of treatment efficacy (ie, 10% and 20% reductions in the HR for the composite endpoint).

The Bayesian analysis included the following steps:

1. Specifying the likelihood function using Phase 3 trial data.
2. Defining the prior distribution based on the Phase 2 trial.
3. Computing the posterior distribution through Bayesian updating.
4. Performing a sensitivity analysis to assess the impact of different prior assumptions.
5. Calculating probabilities of achieving specific efficacy thresholds.

Likelihood Function

The likelihood function, representing the observed data from the Phase 3 trial [5], was assumed to be normally distributed. The observed HR was 0.43. The standard error (SE) was calculated from the observed CI using the following formula: SE = (log(Upper CI) − log(Lower CI) ) ?(2 * 1.96), where upper CI = 1.74, lower CI = 0.11, and 1.96 is the z value corresponding to the 95% CI.

Prior Distribution

The prior information available for our analysis was limited to the Phase 2 study results, which did not include an HR (the measure used in our statistical model’s likelihood function). As a result, an HR was extrapolated from the observed 58.3% responder rate and the prior mean HR was set to 0.6, reflecting an anticipated 40% reduction in hazard. The prior distribution of the log HR (logHR) was assumed to be normally distributed. The prior distribution standard deviation was set to 0.5, indicating moderate uncertainty based on the low number of patients enrolled in the Phase 2 study and variability observed in functional response.

Posterior Distribution

The general Bayesian formula is Posterior ∝ Prior × Likelihood. The posterior distribution and Credible Intervals (CrIs) were calculated using Bayesian updating for normal distributions.

Sensitivity Analyses

To help determine the robustness of the results, sensitivity analyses were conducted to evaluate the impact of varying prior assumptions on the posterior estimates. The classification of priors as informative, optimistic, conservative, and non-informative was based on the characteristics of the prior HR and the SD associated with the prior distribution.

A prior HR value close to the center (0.6) was considered informative. Prior beliefs that the treatment would have a beneficial effect were represented with prior HR values of 0.8 and 0.9, indicating optimism and conservatism, respectively. A prior HR value of 1.0 was used for the non informative prior. For all priors, a moderate SD (0.5) was chosen, reflecting some uncertainty in the treatment effect. This SD signifies that the prior information is less certain, and the resulting posterior HR will be driven more by the data than by the prior.

For each combination of prior HR and SD, the posterior distribution and 95% CrIs were recalculated using the same Bayesian updating formulas.

Probabilities of achieving efficacy thresholds

The probabilities of the true HR being less than specific thresholds (1.0, 0.9, and 0.8) were calculated using Monte Carlo simulations. The simulation of posterior samples generated 100,000 random samples from the posterior distribution. To calculate probabilities, the proportion of simulated HR values less than HR threshold was determined.

Visualization

The likelihood function, prior distribution, and posterior distribution were plotted over a range of HR values (−2.0 to 2.0) using the normal probability density function. The likelihood function was scaled for visualization purposes.

Software and computational tools

All Bayesian computations, sensitivity analyses, and visualizations were performed using R (version [4.4.1]) [8]. The following packages were utilized: ggplot2 (version 3.3.0) for data visualization; reshape2 (version 1.4.4) for data manipulation; knitr (version 1.28) and kableExtra (version 1.1.0) for generating tables; and binom (version 1.1-1) for calculating binomial CIs. The detailed R code is provided in Online Resource 1.

The Bayesian reanalysis yielded a posterior HR of 0.54, indicating a possible 46% reduction in the hazard of worsening heart failure or all-cause mortality compared to control. As shown in Figure 1,

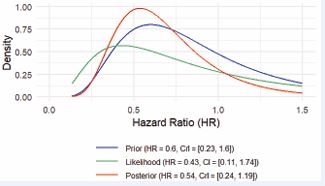
Figure 1 The prior distribution (blue curve) reflects the prior belief about the efficacy of the treatment before observing the Phase 3 trial data. The HR from prior knowledge is 0.6, with a CrI of 0.23 to 1.60. The likelihood distribution (green curve) is derived from the Phase 3 trial data alone. The observed HR is 0.43, with a CrI of 0.11 to 1.74. This likelihood curve is wider than the prior distribution, indicating less confidence from the new data but still showing overlap with the prior belief. The posterior distribution (red curve) is the result of combining the prior belief (blue) and the new data (green). The updated HR is 0.54, with a CrI of 0.24 to 1.19. The posterior distribution is narrower than the prior, indicating that the analysis has reduced uncertainty by incorporating the new trial data. However, there is still uncertainty as the CrI crosses 1, meaning it is plausible that the treatment will not have a strong effect. Abbreviations: CrI: Credible Interval; HR: Hazard Ratio.

the posterior HR (0.54) lies between the prior (0.6) and the likelihood (0.43) distributions, suggesting that the new data has moderated the prior belief, resulting in a more balanced estimate. The posterior CrI of 0.24 to 1.19 does not exclude 1, which implies that the treatment effect, while likely beneficial (HR < 1), is not statistically certain.

Based on the analysis, there was a high probability (93.75%) that the treatment is effective (HR < 1; Figure 2).

Figure 2 Probability of any efficacy (HR < 1) The red dashed vertical line at HR = 1 separates the region where the HR indicates a treatment benefit (HR < 1) from where the treatment might not have an effect (HR ≥ 1). The shaded area under the curve is proportional to the probability of any efficacy and demonstrates that, based on the analysis, there was a high probability (93.75%) that the treatment is effective (HR < 1). Abbreviation: HR: Hazard Ratio.

As the efficacy threshold became more stringent (ie, HR < 0.9 and HR < 0.8), the probability of achieving the reduction decreased (Table 1),

Table 1: Probability of any (HR < 1), 10% (HR < 0.9), and 20% (HR < 0.8) efficacy, including sensitivity analyses.

To help determine the robustness of the results, sensitivity analyses were conducted to evaluate the impact of varying prior assumptions on the posterior estimates. The classification of priors as informative, optimistic, conservative, and non-informative was based on the characteristics of the prior HR and the SD associated with the prior distribution.

Thresholds < 1, < 0.9, and < 0.8 suggest any, moderate, and high degrees of efficacy, respectively.

Abbreviations: CrI: Credible Interval; HR: Hazard Ratio

reflecting the difficulty of achieving stronger treatment effects. The probability of moderate efficacy (HR < 0.9) and high efficacy (HR < 0.8) was 89.89% and 83.82%, respectively.

Sensitivity Analyses

Sensitivity analyses (Table 1), demonstrated that the posterior estimates are influenced by the choice of prior parameters. Stronger prior beliefs in efficacy (lower prior HR) lead to lower posterior HR estimates, suggesting greater treatment efficacy.

This reanalysis of the Phase 3 trial for ARRY 371797 in LMNA-related DCM using Bayesian methods offers several important insights that highlight both the utility and challenges of Bayesian approaches in rare disease clinical trials.

Based on interim data, the original frequentist analysis concluded futility, with an HR of 0.43 and p-value of 0.23, which did not reach statistical significance. However, the Bayesian reanalysis presents a more nuanced view, uncovering potential efficacy signals that were previously obscured. Specifically, by incorporating prior information from the Phase 2 trial, where a 58.3% responder rate was observed, the Bayesian approach reveals a >80% probability of achieving a 20% reduction in the HR, suggesting a high chance of achieving this level of efficacy and that the treatment provides a clinically meaningful reduction in risk. This demonstrates how Bayesian methods can enhance interpretation of available data by integrating prior knowledge, thus overcoming some of the limitations of traditional frequentist approaches, particularly in the context of small sample sizes and rare diseases.

The overall interpretation of the results is also affected by the choice of HR thresholds, which are critical for decision-makers (eg, clinicians, regulatory bodies, health technology assessment agencies) when considering what level of efficacy is needed to justify treatment approval, reimbursement, or further investment in the treatment. A treatment might appear efficacious with an HR < 1 but may not reach clinically meaningful thresholds, such as HR < 0.8, which can influence the conclusions drawn about its real-world effectiveness.

One of the key strengths of the Bayesian framework is its flexibility in incorporating prior information. In this reanalysis, the use of various priors (ie, informative, optimistic, conservative, and non-informative) allowed for a thorough exploration of how different assumptions about the treatment’s effectiveness could influence the results. Notably, the informative prior, derived from the Phase 2 trial, provided support for continued belief in the treatment’s potential efficacy. The resulting posterior distribution indicated an HR of 0.54, suggesting that the treatment could reduce the hazard by up to 46%. The conservative prior, meanwhile, tempered the treatment’s perceived efficacy, with a posterior HR of 0.70, reflecting the prior belief’s assumptions.

For rare disease trials, setting relevant outcomes and appropriate inclusion/exclusion criteria is difficult— but crucial to determining a treatment’s efficacy. These challenges are illustrated in the clinical studies of ARRY 371797. The Phase 3 trial authors acknowledge that the chosen measures and biomarkers had not been validated in patients with LMNA-related DCM [5]. Further, the trial enrolled patients with LMNA variants of uncertain significance, contributing to a heterogenous patient population that may have produced the highly variable observed changes in outcomes and limited detection of treatment-related changes [5]. Interestingly, in the Phase 2 long-term extension study that only enrolled patients who might, in the Investigator’s opinion, derive benefit from continued treatment with ARRY-371797 [9], preserved exercise capacity over 144 weeks was demonstrated [10]. This finding supports that better definition of the target population can clarify whether a treatment is beneficial. Overall, these results illustrate that the designation of a treatment as futile may be the product of factors other than the treatment’s efficacy, such as suboptimal outcome measures or a heterogenous patient population.

Rare diseases present unique challenges in clinical trial design, particularly due to small sample sizes, high intrapopulation variability, and the difficulty of replicating findings across larger, more heterogeneous populations. In this setting, traditional frequentist methods often fall short, as evidenced by the Phase 3 trial’s futility conclusion, which may have prematurely dismissed a potentially beneficial treatment.

In comparison, the Bayesian approach allows for a more flexible and adaptive framework that can incorporate prior information and quantify uncertainty more effectively. This is particularly valuable in rare disease trials, where every data point is precious, and small effects may still be clinically meaningful.

The results of this reanalysis suggest that ARRY 371797 may indeed provide a clinically significant benefit to patients with LMNA-related DCM, as evidenced by the high probability of achieving meaningful HR reductions. Such findings have important implications for the design and evaluation of future rare disease trials. By integrating prior knowledge and providing more nuanced assessments of treatment effects, Bayesian methods may help to avoid premature trial terminations and provide patients with better access to potentially life-saving therapies.

Limitations and Considerations

Bayesian analysis is not without its challenges. The choice of prior is a subjective decision that can significantly influence the results. Our prior distribution based on the Phase 2 trial may be overly optimistic due to the lack of a control group and small sample size, which can skew the Bayesian analysis toward indicating efficacy. The findings of the sensitivity analyses highlight the importance of transparent reporting when employing Bayesian methods, to ensure that results are not overly dependent on a single set of assumptions.

Moreover, the Bayesian approach does not eliminate the challenges of small sample sizes and high intrapopulation variability inherent in rare disease trials. Instead, it provides a more flexible framework for managing these issues that still requires careful consideration of prior information and model assumptions.

This reanalysis of data from the Phase 3 trial of ARRY 371797 in LMNA-related DCM demonstrates the potential for Bayesian methods to uncover meaningful insights in clinical studies for rare diseases. By integrating prior knowledge from a Phase 2 trial, the Bayesian approach revealed a high probability of achieving clinically significant HR reductions, despite the frequentist conclusion of futility. While the sensitivity of the results to different priors underscores the importance of careful prior selection and transparent reporting, overall, this study highlights the advantages of Bayesian methods in making better use of limited and uncertain trial data. Moving forward, Bayesian approaches should be considered more frequently in rare disease research, where traditional statistical methods often fail to fully capture the potential efficacy of novel treatments.

Louise Perrault is Founder and CEO of International Market Access Consulting, which supports pharmaceutical and biotechnology organizations in the fields of strategic product positioning, outcomes research, HTA reimbursement, and health economics; no payments have been received from ARRY-371797’s developer. Jacques LeLorier has no competing interests to disclose.

No funds, grants or other support was received. Louise Perrault: Writing- original draft, Validation, Methodology, Investigation, Formal analysis, Data Curation. Jacques LeLorier- review & editing, Supervision.

Supplementary Information

OnlineResource1.pdf − Detailed R code for the Bayesian reanalysis.

1. Orphan Drug Act (Public Law 97-414): 21 USC 360bb. 1983.
2. Regulation (EC) No 141/2000 of the European Parliament and of the Council of 16 December 1999 on orphan medicinal products. Official J European Union. 2000; 18: 1-5.
3. Fonseca DA, Amaral I, Pinto AC, Cotrim MD. Orphan drugs: Major development challenges at the clinical stage. Drug Discov Today. 2019; 24: 867-872.
4. Mitani AA, Haneuse S. Small data challenges of studying rare diseases. JAMA Netw Open. 2020; 3: e201965.
5. Garcia-Pavia P, Palomares JFR, Sinagra G, Barriales-Villa R, Lakdawala NK, Gottlieb RL, et al. REALM-DCM: A Phase 3, Multinational, Randomized, Placebo-Controlled Trial of ARRY-371797 in Patients with Symptomatic LMNA-Related Dilated Cardiomyopathy. Circ Heart Fail. 2024; 17: e011548.
6. MacRae CA, Taylor MRG, Mestroni L, Moses J, Ashley EA, Wheeler MT, et al. Efficacy and Safety of ARRY-371797 in LMNA-Related Dilated Cardiomyopathy: A Phase 2 Study. Circ Genom Precis Med. 2023; 16: e003730.
7. Hasselberg NE, Haland TF, Saberniak J, Brekke PH, Berge KE, Leren TP, et al. Lamin A/C cardiomyopathy: Young onset, high penetrance, and frequent need for heart transplantation. Eur Heart J. 2018; 39: 853-860.
8. R Core Team. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2020.
9. ClinicalTrials.gov. A rollover study of ARRY-371797 in patients with LMNA-related dilated cardiomyopathy.
10. Judge DP, Lakdawala NK, Taylor MRG, Mestroni L, Li H, Oliver C, et al. Long-Term Efficacy and Safety of ARRY-371797 (PF-07265803) in Patients With Lamin A/C-Related Dilated Cardiomyopathy. Am J Cardiol. 2022; 183: 93-98.