Studying Structural Properties of ZnO: Pb3O4 Particles with Different Concentration

Ahmad Khoudro; Sallama Abo Alshamlat; Heleen Massoud*

doi:10.47739/2334-1831/chemistry-10-1060

Studying Structural Properties of ZnO: Pb3O4 Particles with Different Concentration

Short Communication | Open Access | Volume 10 | Issue 1

Article DOI : https://doi.org/10.47739/2334-1831/chemistry-10-1060

Ahmad Khoudro Sallama Abo Alshamlat Heleen Massoud*

^1. Department of physics, Faculty of science, Tishreen University, Syria

+ Show More - Show Less

Corresponding Authors

Heleen Massoud, Department of physics, Faculty of science, Tishreen University, Syria

Abstract

Zno, $\small Pb_{3}O_{4}$ doped tin oxide transparent conducting powder were prepared by solid-state reaction method. Structural properties of the samples were investigated as a function of various Zno, $\small Pb_{3}O_{4}$ doping levels (x=0.0- 0.2- 0.5- 0.8). The results of x-ray diffraction have shown that the samples are polycrystalline structure in tetragonal phase with preferential orientations along the (110) for all samples. The relative intensities, distance between crystalline planes (d), crystallite size (D), dislocation density ( $\small \delta$ ) and lattice parameters (a), (c).

Keywords

Powder, Iron and Antimony doped Tin Oxide, Solid state reaction, Structural properties

Citation

Khoudro A, Alshamlat SA, Massoud H (2023) Studying Structural Properties of ZnO: Pb3O4 Particles with Different Concentration. JSM Chem 10(1): 1060.

INTRODUCTION

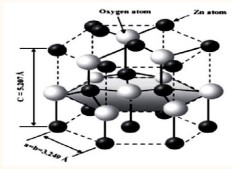
One of the most important semiconductors are the so-called transparent conduction oxides (TCO), which are compound semiconductors composed of metal combined with oxygen, that is, they are oxide conductors as ( $\small SnO_{2}$ , $ZnO_{2}$ , $\small In_{2}O_{3}$ ), and despite their large energy gap, the conduction band is full of free electrons due to the oxygen vacancies resulting from non-stoichiometry [1]. Translucent conductive oxides are characterized by a wide energy band change from 3eV to 5eV. This wide depends on several factors including: the type of solution compounds, deposition method and experimental conditions for sedimentation. One of these oxides is zinc oxide, which is a white, solid, pure compound, yellows on heating due to retinal abnormalities, it is non-toxic substance that does not dissolve in water or alcohol but rather dissolve in acetic acid, mineral acids, ammonia, ammonium carbonate and alkaline hydroxides. In preparing zinc oxide chemically laboratories depend on burning zinc in the air or by thermal smashing of its carbonates or nitrates, (Table 1) shows some of its properties [2]. Zinc oxide crystallizes in a hexagonal lattice, where the oxygen atoms occupy the hexagonal lattice sites, while the zinc atoms occupy half of the quaternary sites. The average constants of the crystal lattice are (a=b 3.25 A0 c=5.206 A0 ). The crystal structure of zinc oxide is similar of the (VI-II) i.e. the hexagonal compact structure as shown in the (Figure 1).

EXPERIMENTAL PROCEDURE

The ZnO: $\small Pb_{3}O_{4}$ surfaces were prepared according to (Table 2) by the solid-state reaction method. They were accurately weighed in the required proportion and were mixed and ground well using an agate mortar to turn them into very fine Powders. Grinding of the mixture was carried out for 3 hours for all powder samples. The samples were placed in an oven at 700C0 for 3
hours in order to obtain the correct crystal structure. (Figure 3, 4)

RESULTS AND DISCUSSIONS

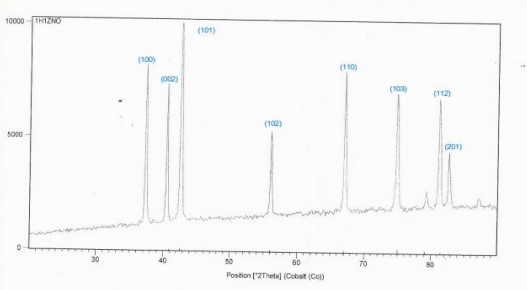
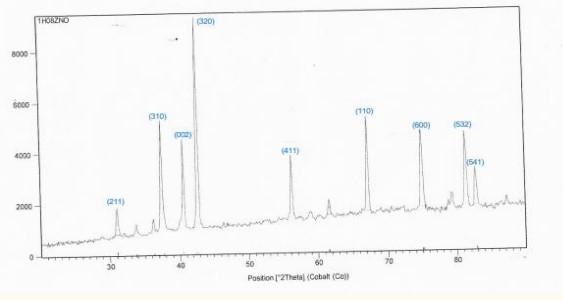
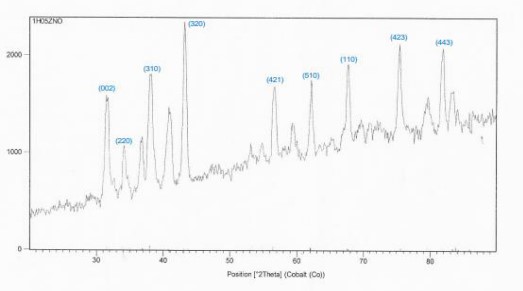
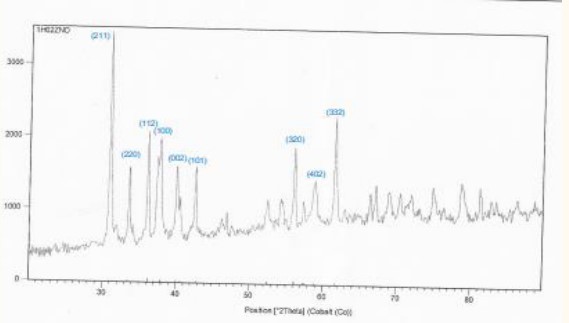
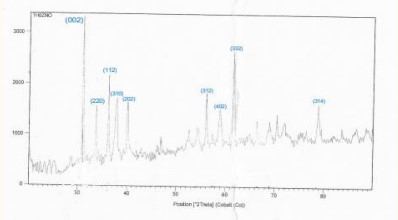
Figure 5, 6 shows: X-ray diffraction patterns for pure $\small Pb_{3}O_{4}$ powders. The XRD reveals that pure Pb3O4 has a quadrangular structure, corresponding to vertices of (002), (112), (310), (202), (312), (402), (332), and (314). The preferred orientation is (002) for pure $\small Pb_{3}O_{4}$ .

We observed the disappearance of these (100), (201), (103), in samples ZnO: $\small Pb_{3}$ .

The change in peak intensity is mainly due to the replacement of $\small Zn^{+2}$ ions by $\small Pb^{+4}$ ions in the ZnO lattice. This process leads to the movement of Zn+2 ions in interstitial sites; in fact, that ionic radius of $\small Zn^{+2}$ iron equals (0.088 nm) is smaller than the ionic radius of $\small pb^{+4}$ (0.0915 nm).

The relative intensities of undoped and Sb doped powders are calculated.

The distance between crystalline planes values (d) are

Table 1: Same Physical and Chemical Properties of Zinc Oxide [3].

Color	The Shape	Boiling Point (C0)	Melting Point (C0)	Density (g/cm3)	Molar Mass (g/mol)	Crystal Structure
White	Solid	2360	1970	5.67	81.37	Hexa

Figure 1: The compact crystal structure of zinc oxide films.

Table 2: Shows the proportions of the prepared samples.

Parcent wt %	$\small Pb_{3}O_{4}$	ZnO	The sample
100	0	1	1
80	0.2	0.8	2
50	0.5	0.5	3
20	0.8	0.2	4
0	1	0

Figure 2: XRD spectra of sample No.1.

calculated by using following relation:

2d.sinθ = nλ (1)

Where d is distance between crystalline planes (A), θ is the Bragg angle, λ is the wavelength of X-rays (λ=1.54056 Å).

The crystallite size is calculated from Scherer’s equation [4]:

$\small D=\frac{0.94}{\beta \cos \Theta }$ (2)

where, D is the crystallite size, λ is the wavelength of X-ray, β is full width at half maximum (FWHM) intensity in radians and θ is Braggs’s angle.

The dislocation density is defined as the length of dislocation lines per unit volume and calculated by following equation [5]:

$\small \delta =\frac{1}{n^{2}}$ (3)

The lattice constants a and c for tetragonal phase structure is determined by the relation [6]:

$\small \frac{1}{d^{2}}=\frac{h^{2}+k^{2}}{a^{2}}+\frac{l^{2}}{^{c^{2}}}$ (4)

where d and (hkl) are distance between crystalline planes and Miller indices, respectively.

Figure 3: XRD spectra of sample No. 2.

Figure 4: XRD spectra of sample No.3.

Figure 5: XRD spectra of sample No.4.

The calculated lattice constants a, c values are given in (Table 3, 4). It was seen that a, c and c/a match well with JCPDS data (a=b= 4.737 Å and c= 3.185 Å). The change in peak intensities is basically due to the replacement of $\small Zn^{+2}$ ions with $\small Pb_{3}O_{4}$ ions in the lattice of the ZnO.

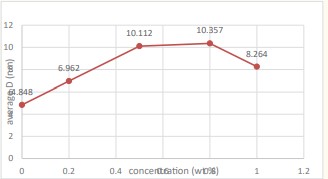
We notice from (Figure 7) that the sample $\small Pb_{3}O_{4}$ ZnO shown in (Figure 2) is the best samples compared to the other samples because the average crystal size is larger and the intensity of dislocations is lower in the crystal lattice.

CONCLUSION

This paper presented a study of the structural properties

Figure 6: XRD spectra of sample No.5.

Figure 7: Represents variation of the average grain size with different concentrations of $\small Pb_{3}O_{4}$ doped ZnO powders.

Table 3: XRD results for sample No.1 form table (2) where θ Bragg angle, D crystal size, d crystal distance, δ dislocation density and int, Miller's integers (hkl) and β width of each pit, a and c are crystal lattice constants.

samples	2θ (deg)	Int	(hkl)	β (deg)	d (Å)	D (nm)	$\small \bar{D}$ (nm)	$\small \delta =10^{+15}X line/m^{2}$	$\small \delta =10^{+15}X line/m^{2}$	Lattic conste
samples	2θ (deg)		(hkl)	β (deg)	d (Å)	D (nm)	$\small \bar{D}$ (nm)	$\small \delta =10^{+15}X line/m^{2}$	$\small \delta =10^{+15}X line/m^{2}$	$\small AA^{0}$	$\small CA^{0}$
$\small Pb_{3}O_{4}$ Pure	3	100	-2	0.4	3.456	4.352	5.059	52.798	42.207	8.855	6.912
	33.2	47	-220	0.3	3.131	5.849		29.23
	35.9	65	-112	0.3	2.902	5.892		28.805
	37.3	52	-310	0.4	2.797	4.437		50.795
	40.2	49	-202	0.4	2.603	4.476		49.913
	55.9	56	-213	0.3	1.908	6.346		24.831
	58.8	46	-402	0.5	1.828	3.86		67.711
	61.4	81	-332	0.4	1.752	4.889		41.836
	78.5	49	-314	0.4	1.414	5.425		33.94

Table 4: XRD results for sample No.2 form table (2) where θ Bragg angle, D crystal size, d crystal distance, δ dislocation density and int, Miller's integers (hkl) and β width of each pit, a and c are crystal lattice constants.

samples	2θ (deg)	Int	(hkl)	β (deg)	d (Å)	D (nm)	$\small \bar{D}$ (nm)	$\small \delta =10^{+15}X line/m^{2}$	$\small \delta =10^{+15}X line/m^{2}$
										Lattic conste
										$\small AA^{0}$	$\small CA^{0}$
$\small ZnO:Pb_{3}O_{4}$ 80%W	30.9	100	-2	0.35	3.354	4.986	5.655	40.225	40.376	8.779	6.714
	33.5	47	-220	0.25	3.104	7.025		20.263
	36.2	61	-112	0.25	2.879	7.077		19.966
	38	58	-100	0.4	2.747	4.446		50.589
	40.2	46	-2	0.25	2.603	7.163		19.489
	42.9	46	-101	0.25	2.446	7.227		19.146
	56.1	55	-320	0.5	1.902	3.811		68.852
	58.9	42	-421	0.6	1.819	3.219		96.506
	61.8	67	-332	0.33	1.742	5.939		28.351
$\small ZnO:Pb_{3}O_{4}$ 20% W	31.1	20	-2	0.33	3.336	5.288	6.504	35.761	26.453	8.876	6.672
	37.2	57	-310	0.3	2.804	5.914		28.591
	40.3	44	-2	0.2	2.596	8.956		12.467
	42.6	100	-320	0.25	2.462	7.229		19.135
	57.2	42	-411	0.4	2.033	4.681		45.637
	67.3	56	-110	0.25	1.614	8.081		15.313
	75	51	-600	0.35	1.469	6.056		27.266
	81.3	49	-532	0.33	1.373	6.716		22.171
	83	35	-541	0.4	1.349	5.613		31.74

of ZnO and $\small Pb_{3}O_{4}$ compounds: prepared by solid state reaction method [7]. The X-ray diffraction patterns of the pure zinc oxide sample confirm that it is of poly crystalline nature and hexagonal compact structure and shows the presence of trends (110), (101), (002) and (101) [8]. The preferred orientation is (101), but for ZnO sample similar to $\small Pb_{3}O_{4}$ by (50-80) % wt.

The preferred trend changes to the (320), and we observed the disappearance of these trends (100), (201), (103) in the ZnO: $\small Pb_{3}O_{4}$ [9-14].

The average crystal size is within the range (4.848-8.264 nm) for all samples. It was determined that the lattice constants c and a for all samples, were the ratio remained constant with the increase of the dopant concentration $\small Pb_{3}O_{4}$ .