Abdominal Aortic Aneurysm (AAA) is a chronic disease in which the abdominal aorta expands until it ruptures. AAA incidence: 10 million/year (India), deaths: 40%-90% (13th leading cause of death in the USA). Current treatment methods make diagnosis difficult due to the lack of noticeable symptoms and inaccurately planned operations. Rupture Scope is a mathematical model to dramatically reduce AAA deaths and improves treatment efficiency. Using a case-specific replica/simulation of real-time abdominal aortic blood flow for monitoring without frequent imaging scans and a novel derived mathematical linear regression model to predict rupture date and expansion rate with an overall accuracy of 90%.

• Abdominal Aortic Aneurysm; Mathematical Linear Regression; Computational Fluid Dynamics; Dynamical Systems

Deouskar A, Agrawal D (2024) A Novel Mathematical Approach with a Correlating Computational Framework for Precisifying Aneurysmal Therapeutics. JSM Math Stat 6(1): 1020.

Abdominal Aortic Aneurysms (AAA) are local enlargements of the abdominal aorta, occurring below the renal bifurcation. These are a prevalent cardiovascular health disease, affecting 35.12 million individuals globally and leading to death of around 200,000 patients per year. Causes include tobacco induction, hypertension, and genetic factors. AAA ruptures results in rapid hemorrhagic shock and multiple lower body organ failures. The main organs dependent on the blood sup- ply by the abdominal aorta, such as kidneys and parts of the alimentary canal, can fail if the abdominal aorta ruptures. Currently, all known treatments for AAA are surgical, including open surgical repair and endovascular surgery. In human anatomy, the abdominal aorta is the largest artery in the human body. In the abdominal cavity the aorta branches out, which form an extensive network supplying blood to the stomach, liver, pancreas, spleen, small and large intestines, kidneys, reproductive glands, etc. [1].

Flaws in Current Therapeutics

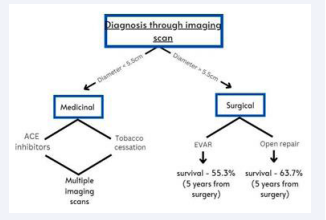
After consulting experienced cardiothoracic surgeons (see Acknowledgments) and asking them about the current course of treatment for AAA, we formulated the following gaps in current therapeutics for AAA: 1) After performing CT, MRI or other imaging tests doctors determine the diameter of the abdominal aorta; (i) If the diameter is larger than 5.5 cm, doctors carry out invasive treatment, (ii) If the diameter is smaller than 5.5cm, the doctors perform drug regulation by using ACE inhibitors to regulate blood pressure, and suggest no further tobacco consumption. 3) To predict the date of rupture and rate of expansion, doctors use their clinical experience, largely based on the observations of previous patients, which has been proven to be mostly inaccurate

· Surgical intervention for AAA poses a serious threat to the individual’s life because EVAR and open repair are extremely complicated surgeries with survivability rates of around 55.3% (EVAR) and 63.7% (open repair), respectively, so a long-run prediction is required to give doctors an idea of whether to ”intervene or not.”

· AAA growth patterns are extremely unpredictable as they can vary hugely in both the cases; 1) sudden increase in expansion rate, 2) sudden decrease in expansion rate, which can sometimes lead to mistreatment of AAA.

· There is a high chance that abdominal aorta could rupture before getting up to the diameter of 5.5cm (3% - 15% according to American Association for Vascular Surgery), and doctors rely solely on this benchmark for the surgical treatment which proves to be highly ineffective and a major cause of death from AAA therapeutics.

The solution consists of a computational frame- work that has the potential to reduce the fatalities of AAA therapeutics drastically. Using a real- time digital simulation of blood flow based on the geometry of the patient’s abdominal aorta and a mathematical model to predict abdominal aortic ruptures and expansion rate with a validated accuracy of 93%. This model will enhance the accuracy of the therapeutics to save multiple lives from the procedure by removing human-estimation based practices.

The model is mainly divided into two major parts i.e. simulation and mathematical model. The following steps depicts the detailed prototype generation of both the parts. No human sample was taken in the process and imaging scans and other statistical data was acquired from online repositories. Further details regarding the sources can be found in the references page.

3D Modeling and Reconstruction

Aim: To digitally reconstruct a 1-1 replica of the patient’s Abdominal Aorta on the basis of geometrical data acquired through a CT scan to create a mesh for the simulation [2].

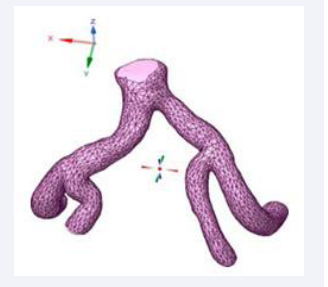
Utilizing Computed Tomography (CT) abdomen scans procured from online repositories such as 3D Embody and the NHIA database in NRRD file format with sagittal, axial and coronal view of abdomen CT. A meticulous 1-1 reconstruction of the abdominal cavity of patients was meticulously orchestrated employing the open-source software known as 3D Slice ran advanced tool designed for scientific data visualization (Figure 1).

Figure 1: Graphical representation of AAA therapeutics.

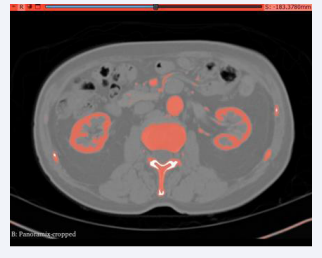
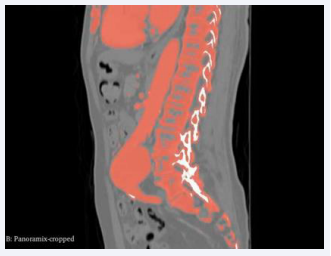
The CT scans were seamlessly imported into 3D Slicer, where a distinctive segment dedicated to the abdominal aorta was meticulously delineated within the ”segmentations” module. The following figure depicts the abdominal aortic segments in axial and sagittal CT scans.

An additional extension employing the “fast marching” algorithm was incorporated. The maximum pre-initialization volume for fast marching was meticulously set at 1%, while the segmentation volume was judiciously established at 67% to achieve an optimal balance between detail and accuracy in modeling the abdominal aorta. A smoothing kernel size of 5.00 mm (or 5x3x3 pixels) was applied, utilizing a ”Median” smoothing median, to eliminate extrusions while preserving anatomical fidelity (Figure 2).

Figure 2: Axial Segmentation.

The resultant model of the abdominal aorta was subjected to meticulous rendering. Extraneous particles and glitches originating from the CT scans were systematically expunged through manual intervention, employing the segment crop tool to ensure a pristine representation of the abdominal aorta.

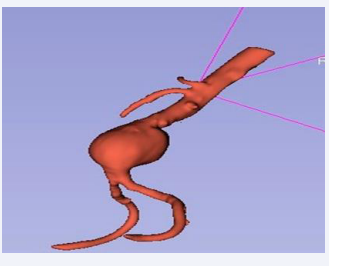
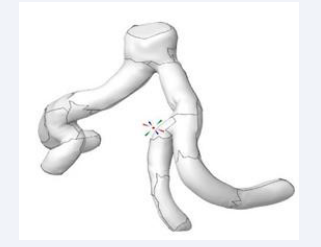
However, for the purpose of simulation, it was imperative to transform the non-hollow model into a hollow one. To accomplish this, an additional ex- tension was employed, featuring a ”hollow” tool with a specified shell thickness of 3.00 mm (or 3x3x3 pixels). The existing segment served as the” inside surface” for this operation, culminating in the successful hollowing of the abdominal aorta and rendering it amenable to simulation processes. Furthermore, the intricate bifurcation of the abdominal aorta, specifically the iliac bifurcation, was meticulously isolated. This anatomical feature was characterized by a single inlet and four outlets (Figure 3-6).

Figure 3: Sagittal Segmentation.

Figure 4: Reconstruction of the abdominal aorta.

Figure 5: Source volume panoramic cropped.

Figure 6: Reconstruction of hollow iliac bifurcation.

Leveraging the Vascular Modeling Tool Kit (VMTK) extension, the geometric dimensions of the iliac bifurcation were extracted to facilitate the subsequent development of the mLR model [3].

The meticulously acquired geometry of the iliac bifurcation was ultimately exported in STL file format. This intricate process reflects a sophisticated integration of medical imaging, mathematical algorithms, and specialized software tools within the realm of academic exploration and biomedical engineering.

Mesh Generation and Simulation Solving

Aim: To generate a real-time simulation implying CFD, FEA to give the visual data of the abdominal aorta and display the pressure gradient, velocity streamline and eddy’s viscosity of the abdominal aorta.

The geometric data of the iliac bifurcation, initially presented in STL (standard triangle language) format, underwent meticulous correction of facet and node alignments using the gmsh software which is finite-element mesh generator. Subsequently, the refined STL geometry was introduced into Mesh Lab (a 3D mesh processing software system) where comprehensive checking and repair algorithms were executed. In addition, mesh element size and density reduction were imperative, prompting the application of Quadric Edge Collapse Decimation (QECD) twice, initially targeting 10,000 facets and subsequently 5,787 facets, effectively mitigating file complexity (Figure 7).

Figure 7: VMTK processing pathway on hollow iliac bifurcation.

The resultant STL file was then imported into Free CAD [4].

(A general-purpose parametric 3D computer-aided design modeler) wherein the conversion of the STL format into a solid with distinct hollow and outer components was achieved through the deployment of the part tool. The ensuing STEP (ISO 10303) file derived from this process was deemed essential for subsequent simulation endeavors (Figure 8-10).

Figure 8: Geometry correction results of gmsh.

Figure 9: The result of STEP conversion from Free CAD.

Figure 10: Before facet merging

This STEP file was imported into Ansys Space Claim 2024 R1, in which the geometry was checked and perfected. To reduce the number of triangles or facets, an intricate method of selecting multiple triangles on a same plane and merging them together to give a single plane was performed for the ease of mesh generation. Thus reducing the number of facets form around 5787 to 40. This geometry was later downloaded in SCDOC format (Figure 11,12).

Figure 11: After facet merging.

Figure 12: Sizing of the sphere of influence to reduce cell count.

In Ansys workbench, the SCDOC geometry was imported into the Fluid Flow Meshing tool. There were total of 2 sizing enhancements and 1 inflation procedure performed in the mesh. First sizing included defining the element size to 1 cm and second sizing involved the input of a sphere of influence with radius 20 cm and element size 0.5 cm. This was necessary because the overall cell count of the mesh was exceeding the maximum limit of cell count of Ansys Student which is 1048567 numbers of cells; the centre of the sphere of influence was taken as the centre of a newly defined Cartesian/coordinate system which stood between the two major branches of the iliac bifurcation. Inflation was used to define the boundary, inlets and outlets of the fluid domain. After all this, the mesh was generated and was ready for CFD simulation (Figure 13).

Figure 13: Defining parts of the fluid domain like inlet and outlet using inflation segments.

The subsequent phase involved defining the physics for simulation within the Andy’s Fluid Flow (Fluent) Parallel Fluent environment. This commenced with the rigorous characterization of blood and its pertinent properties, encompassing density (1060 kg/m3 ), specific heat (1006.43 J/kgK), thermal conductivity (0.0242 W/mK), and viscosity (1.7894e-05). These values were meticulously derived from an extensive analysis of blood properties documented in diverse medical journals. Inlet and outlet conditions were established, incorporating boundary conditions from named selections acquired during the pre-meshing inflation process. In the inlet, the temperature was stipulated at 310 K, coupled with a velocity magnitude of 0.3 m/s. Hybrid initialization facilitated the commencement of physics setup calculations, furnishing the requisite framework for simulation (Figure 14).

Figure 14: Generated mesh of iliac bifurcation.

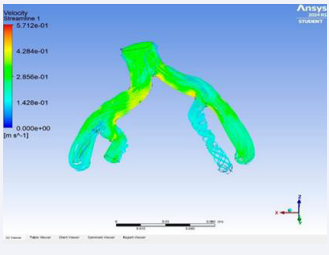
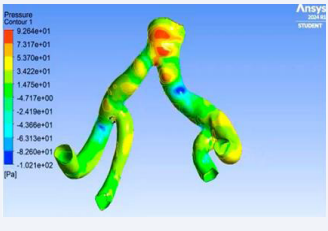
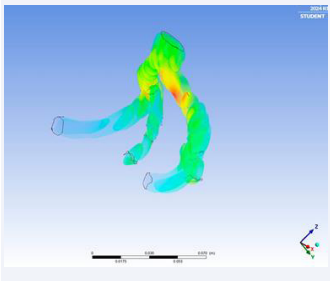
The solution gave the real-time visualrepresentation of the velocity streamline of blood flow, pressure contour on the arterial wall and Eddy’s viscosity.

Notably, the simulation solver settings introduced a pioneering element, wherein the mLR model’s direct outcomes governing the abdominal aorta’s expansion rate were implemented. This dynamic model, boasting 95.64% accuracy, facilitated real-time alterations in the size and geometry of the abdominal aorta, concurrently revealing prospective rupture locations through pressure contour analysis.

The fundamental mathematical governing equations that solved the simulation are the following;

· Continuity Equation:

Where; ρ is density; ∇ is vector differential operator; is rate of change in density.

· Navier Stokes Equation:

Where; v is the velocity of the fluid; t is time; ∇ is gradient of the pressure; µ is fluid’s resistance to flow; f is external force acting on the fluid.

Mathematical Linear Regression (mLR) Model for Rupture Prediction

Aim: The aim was to create a mathematical formula that could forecast the rupture date, expansion rate, and enlarged size of the abdominal aorta based on statistical data that is bio-mechanical parameters and geometrically studied variables (Figure 15).

Figure 15: Velocity streamlines demonstration.

Upon a comprehensive examination of the biomechanical aspects pertaining to the Abdominal Aorta and the systematic elucidation of specific biomechanical determinants influencing Abdominal Aortic Aneurysm (AAA) rupture, a formulation has been devised for the computation of the augmented dimensions of the abdominal aorta following a time interval denoted as ’t’. Through nuanced adjustments, this formulation enables the calculation of the expansion rate of the abdominal aorta, facilitating the prognostication of the potential rupture date. The paramount biomechanical factors incorporated into the model include:

• Compliance- which defines as the change in volume occurs with respect to the change in pressure of the Poisson’s Ratio- which is the ratio between transverse contractions to longitudinal extension strain.

• Elastic Modulus- which is the resistance of material to deformation.

• Laplace Law- which states that the arterial wall tension is proportional to the vessel radius for a given blood pressure.

The following is the numerical representation of compliance (C);

C = ?V

?P

but in the case of arterial environment;

C = Vd – Vs

Ps − Pd

Where; Vd is diastolic volume; Vs is systolic volume; Ps is systolic pressure; Pd is diastolic pressure.

Numerical representation of Poisson’s ratio (V);

Where; d?trans is the transversal strain and d?axial is the axial strain.

Numerical representation of Elastic Modulus (E)

But in the case of arterial environment;

Where; Vo is volume, Rav is radius, v is Poisson’s ratio; h is arterial wall thickness and C is compliance of arterial wall.

The variables in the formula are geometrical basis of abdominal aorta, which are obtainable from the previously mentioned steps. The following is the derived novel formula:

Where;

x = expanded diameter after 1 second of time;

y = diameter before 1 second of time;

Vo = diastolic volume;

Rav = diastolic radius;

l o = systolic lateral length;

l = diastolic lateral length;

d = diastolic axial length;

do = systolic axial length;

h = wall thickness;

p = blood pressure mean

Upon the multiplication of the variable de- noted as ’x’ with the temporal interval, expressed in seconds, the resultant product yields the diameter magnitude subsequent to the stipulated time duration. Concurrently, by dividing the temporal parameter into this product, the expansion rate, denoted as growth per unit time, is discerned. Given the chronic nature of Abdominal Aortic Aneurysm (AAA), the recommended unit for quantifying the expansion rate was ascertained to be ”growth/year.” Leveraging the thickness of the arterial wall (h) and elucidating its correlation with the diameter, temporal predictions regarding the potential rupture event are attainable. The prescribed mathematical formulation has been implemented in Python to facilitate the computational procedure (Figure 16,17).

Figure 16: Pressure contour across arterial wall.

Figure 17: Eddy’s viscosity in volume of abdominal aorta.

Notably, the regular inclusion of blood pressure (p) as input serves to mitigate inaccuracies arising from variable factors. It is imperative to underscore that the Python source code necessitates the contemporaneous input of the prevailing blood pressure value prior to any result compilation.

To assess the efficacy of the model, a cohort of 10 Computed Tomography (CT) scans was procured from the publicly accessible online repository, 3D embody. Geometrical analysis, facilitated by Vascular Modeling Toolkit (VMTK) processing, was employed to ascertain the variable values. Presented below are five among the ten experimental outcomes.

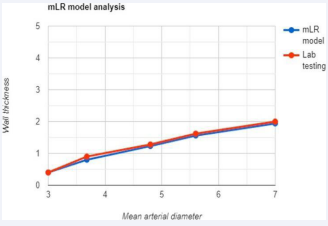
Using these results the overall accuracy of the mLR was found out to be of 95.64% with respect to the lab testing values.

• Using the simulation, the real-time blood flow in the iliac arteries was simulated giving us eddy’s viscosity, velocity streamline and pressure contour of the aortic flow. Using these factors, we were able to locate the high-stressed regions in the aortic wall which are prone to rupture. We were also able to monitor the structural changes in the abdominal aorta with respect to time with the aid of the simulation.

• The structural changes displayed a slow increment in the mean diameter overtime and a steady decrease in the wall thickness. This was found out to be correct using the Laplace’s law, a bio-mechanical law stating that diameter of a vessel is inversely proportional to its wall thickness i.e. as diameter increases, the wall thickness decreases.

• The mLR model’s overall accuracy was of 95.64% with the use of a single CT scan with respect to lab testing, which requires results from multiple imaging scans. For visual understanding of the accuracy of the mLR, a linear graph was plotted from the values of (Table 1), (Graph 1).

Table 1: Comparison of rupture scope mLR and lab testing expansion rate values using real-life value sets.

Variable values used	Results from mLR	Results from lab testing
WT -4.25 mm	0.4 mm/year	0.4 mm/year  ?
ID- 3 cm
BPm - 73 mm hg
IL - 13 cm
WT- 3.98 mm	0.8 mm/year	0.9 mm/year
ID- 3.68 cm
BPm- 82 mm hg
IL- 13.23 cm
WT- 2.8 mm	1.23 mm/year	1.28 mm/year
ID- 4.8 cm
BPm-74 mm hg
IL- 13.3 cm
WT- 2 mm	1.56 mm/year	1.62 mm/year
ID- 5.6 cm
BPm- 102 mm hg
IL- 13.5 cm
WT - 1.4 mm	1.94 mm/year	2 mm/year
ID - 7 cm
BPm - 115 mm hg
IL - 14.2 cm

Where;

WT = Arterial wall thickness

ID- Mean initial diameter

BPm = Blood Pressure mean

IL – lateral length during diastole

Graph 1: Linear graph comparing mLR and lab results.

The Rupture Scope system integrates a parallel blood flow simulation and the mLR model through continuous data exchange. Geometric alterations are observed by the simulation, and these values are subsequently communicated to the mLR’s code. When coupled with an individual’s blood pressure, the system forecasts the expansion rate and potential rupture date. The expansion rate is then incorporated back into the simulation, alongside the current blood pressure, facilitating the visualization of size changes and identification of high-stress regions in the aortic wall. This establishes a robust and precise framework, significantly reducing fatalities associated with Abdominal Aortic Aneurysm (AAA) therapeutic procedures and enhancing procedural efficiency.

The following are the ways in which Rupture Scope is going to benefit the patients and doctors:

• The knowledge of the date of rupture helps out in planning the surgical intervention. Currently, doctors perform human estimation for the prediction of expansion rate and rupture date which is mostly inaccurate but Rupture Scope’s mLR resolves the issue by using statistical data related to the bio-mechanical properties of the specific patient’s abdominal aorta making it case- specific and accurate.

• As of now patients are suggested to have an imaging scan on an yearly basis giving us an average of 5-6 scans, by using Rupture Scope framework this number can be reduced to as low as 2 scans reducing the treatment cost and individual’s exposure to radiation.

• The knowledge of high-stressed regions will tremendously help in the planning of EVAR surgery by providing accurate measurements for stent-graft placement, thus minimizing fatalities from improper stent-graft placements.

• Proper stent-graft placement requires de- tailed measurements of the abdominal aorta from celiac trunk to iliac bifurcation; these are measured from imaging scans using practices which have a chance of human error. Rupture Scope, eradicates this problem by automation on validated framework.

• The surgeries are performed on the basis of diameter benchmark of 5.5cm, but there is a high probability of the abdominal aorta ruptured before attaining a diameter of 5.5cm. Hence, the accurate factor of determining the time of intervention is arterial wall thickness.

The Rupture Scope framework represents a sophisticated integrative platform leveraging state of the art computer science and mathematical methodologies within the field of biomedical sciences. Its primary objective is to refine treatment approaches, significantly reducing mortality rates and promoting global health preservation. This innovative tool, designed for utilization by cardio- thoracic surgeons worldwide, is poised to have a profound impact on mitigating fatalities associated with Abdominal Aortic Aneurysm (AAA). Validation of the Rupture Scope has been under taken using curated datasets from open-source repositories, and project deliberations have undergone scrutiny by certified cardio-thoracic surgeons, affirming its utility. Future endeavours involve conducting extensive validation through collaborative associations with hospital entities. This endeavour represents a pioneering contribution, drawing from comprehensive sources to comprehend AAA-related challenges and elucidates the biomechanical intricacies of the abdominal aorta.

We would like to acknowledge our mentor, Mr. Sushil Kumar Pandey, for helping with the formatting of the project and guidance with the overall perspectives. We also acknowledge our institution for providing us the opportunity for conducting this research. We also acknowledge all the cardio-thoracic surgeons Dr. Vinod Ahuja (MBBS, MS, MCh) “Cardiothoracic and Vascular Surgery“(Chief cardiothoracic surgeon, Ramakrishna Care group of hospitals, Raipur). Dr Kshitij Dubey (MBBS, MS, MCh) “Cardiothoracic and Vascular Surgery” (Chief cardiothoracic surgeon, Apollo group of hospitals, Indore). Dr. Ajay Chourasia (MBBS, MS, MCh) “Cardiothoracic and Vascular Surgery” (Chief cardiothoracic surgeon, SMC cardiac centre, Raipur). We acknowledge Dr. Nicolas Alexander Weiss (BSc Mathematics, Jacobs University Bremen and student of the Berlin Mathematical School and completing MSc in Mathematics at Humboldt University at zu Berlin. For the validation of our mLR model to be mathematically correct.

1. van ‘t Veer M, Buth J, Merkx M, Tonino P, van den Bosch H, Pijls N, et al. Biomechanical properties of abdominal aortic aneurysms assessed by simultaneously measured pressure and volume changes in humans. J Vasc Surg. 2008; 48(6): 1401-1407. doi: 10.1016/j. jvs.2008.06.060. Epub 2008 Sep 4. PMID: 18771885.

2. Wilson K, Bradbury A, Whyman M, Hoskins P, Lee A, Fowkes G, et al. Relationship between abdominal aortic aneurysm wall compliance and clinical outcome: a preliminary analysis. Eur J Vasc Endovasc Surg. 1998; 15(6): 472-427. doi: 10.1016/s1078-5884(98)80105-6. PMID: 9659880.

3. Scotti CM, Shkolnik AD, Muluk SC, Finol EA. Fluid-structure interaction in abdominal aortic aneurysms: effects of asymmetry and wall thickness. Biomed Eng Online. 2005; 4: 64. doi: 10.1186/1475- 925X-4-64. PMID: 16271141; PMCID: PMC1298313.

4. R. Kosasih. 3D reconstruction of abdominal aortic aneurysm using Laplacian Eigenmaps. AIP Conf Proc. 2023; 2431.