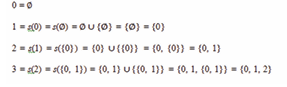This article investigates the concept of “nothing” as the foundational entity in mathematical structures, starting with the concept of the void, as in the beginning (Genesis), there was emptiness (void). By considering the void as a primal entity in mathematics, we show how its existence is central to the construction of the number system/concept of infinity, set theory, and other mathematical concepts such as void’s role in topology and logic. Through the careful examination of basic operations, sets, and structures, we demonstrate that “nothing” can give rise to something which, in turn, gives rise to everything. The article concludes with a discussion on the necessity of “nothing” in both mathematical abstraction and practical application.

• Void

• Set theory

• Numbers

• Infinity

Odizilike KN (2025) Everything I Know About Nothing: a Mathematical Exploration of the Void and its Role in Constructing Mathematics. JSM Math Stat 7(1): 1021.

Mathematics is often seen as a pursuit of understanding existence through numbers, shapes, and structures. However, at its core, mathematics also rests on understanding what “nothing” is. Thinking about nothing gives it the name “void”. But then, is void nothing?. The answer to this will be given later in the write up. We claim the void, often symbolized as ∅ or {}, forms the bedrock of set theory and by extension, most of modern mathematics.

Zero on the other hand is often considered the most paradoxical and elusive number in mathematics. It holds profound implications across various domains of mathematics, philosophy, and even science. Thus, the title “Everything I Know About Nothing” plays on the curious relationship between zero/empty set and the concept of existence. At first glance, “nothing” seems to be the absence of everything, but through the lens of mathematics, zero proves to be a cornerstone in the creation of everything.

The Birth of Nothing (Zero)

Zero was a revolutionary concept in mathematics. Early civilizations, such as the Babylonians, had symbols for nothing but did not fully integrate it as a number. Robert [1], suggests that the first recorded use of zero appeared in Mesopotamia around 3 B.C. The Mayans independently invented it circa 4.

A.D. By the mid-5th century, Indian mathematicians like Aryabhata and Brahmagupta had begun using zero as a placeholder in calculations. Zero spread to Cambodia by the late 7th century, to China and the Islamic world by the late 8th century, and reached western Europe in the 12th century.

The birth of zero gave meaning to the operations of addition, subtraction, multiplication and division by zero. Without zero, we wouldn’t have place value or the ability to express large numbers, which are foundational to all fields of mathematics. Hence, it suffices to say the following;

• The birth of zero is the building block of arithmetic.

• Zero in algebra is the creation of solutions and

• Zero in calculus is the gateway to the infinite

The Void and the Creation of Numbers

To begin, consider the empty set ∅ as a representation of ’nothing’ and define zero as the cardinality of the empty set:

0 = |∅| (1)

Equation (1) illustrates that “nothing” is not merely an absence but the starting point for building the number system and the empty set is not the same thing as nothing;

rather, it is a set with nothing inside it and a set is always something. It follows immediately that {∅} ?= ∅, which establishes the concept that two things can be distinct. By implication, ’nothing’ is not the same as ’void’; rather, ’nothing’ gives rise to the concept of ’void’. Since ’nothing’ is not equivalent to the ’void’, it is reasonable to conclude that the ’void’ is a state that embodies ’nothingness’, that is, void is something that is nothing [2].

This initial concept of ’nothing’ allows us to define the subsequent natural numbers through the Peano axioms [3], starting with 0 and using the successor function S(x). In essence, the standard construction of the naturals starts from Equation (1) and the operator s defined as;

s(a) = a ∪ {a) (2)

We can then define the set of natural numbers N as the intersection of all sets closed under s that contain the empty set. Each natural number is equal (as a set) to the set of natural numbers less than it. It follows from Equation (2) that;

and so on. This shows that the void is not just an absence, but a productive entity, generating an infinite sequence of numbers. The construction of integers, rational numbers, and real numbers follows a similar pattern of abstraction from this empty starting point. For instance, the set of integers can be constructed as pairs of natural numbers, and the rational numbers as ordered pairs of integers. Thus, every number in our system derives from the void, a proof that everything can be made from nothing.

The empty set, having no members, is considered a subset of every ordered set, where every member serves as both an upper and lower bound for the empty set. For example, in the real numbers with the usual ordering, every real number is both an upper and lower bound for the empty set. Similarly, in the extended reals, which include negative infinity (−∞) and positive infinity (+∞), every.

element of the set is also an upper and lower bound for the empty set. So, we have that;

sup ∅ = min({-∞, +∞}∪R) = ∞ (3)

inf ∅ = max({-∞, +∞}∪R) = ∞ (4)

From Equation (3), we see that the empty set, though representing “nothing,” defines boundaries like −∞ and +∞, showing its role in mathematical structures. Philosophically, the empty set challenges the concept of existence, illustrating how “nothing” can have meaningful influence in constructing mathematical reality. Recall that in the foundational work of mathematicians like Cantor, Zermelo, and Hilbert, it was proposed that all of mathematics can be built upon set theory. Thus, if void is a foundational element in set theory, it can be seen as a building block for the entire structure of mathematics and its construction.

The Void in Logic, Topology, and Category Theory

In logic, the void represents falsity, symbolized by ⊥ (bot), and serves as the foundation for logical systems. From this negation, truth tables and formal reasoning structures are constructed, with “nothing” as the starting point for logical frameworks [4]. In classical logic, the operations of negation, conjunction, disjunction, and implication are all built upon the idea of truth and falsity. The negation of a proposition, denoted as ¬P, takes the truth value of a statement and flips it. If a proposition is true, its negation is false, and if a proposition is false, its negation is true. The falsehood or falsity (⊥) is the basic element from which these operations emerge.

For example, in propositional logic, the truth table for negation demonstrates how the truth value of a proposition is inverted:

• If P is true, then ¬P is false (⊥).

• If P is false (⊥), then ¬P is true.

In topology, the void is represented by the empty set, which is both open and closed (clopen) in any topological space. It is also compact, as all finite sets are compact. By considering the empty set as an open set, we can build complex topological structures through operations like closure, boundary, and interior.

In category theory, the empty set is the unique initial object in the category of sets and functions.

It also serves as the initial object in the category of topological spaces when defined as an open set, with a unique function mapping the empty set to itself. This highlights the void’s foundational role in structuring mathematical systems.

From logic to topology and category theory, the void is not merely an absence but a foundational element that enables the construction of complex mathematical systems. Through the void, we see how “nothing” can be transformed into a powerful tool for understanding and defining the very nature of mathematical reality.

Some Proofs and Theorems

We now provide a few essential results that demonstrate the role of “nothing” in constructing mathematics.

Theorem 1: Zero is the identity element for addition.

Proof: By the Peano axioms [3], we define addition recursively:

x + 0 = x, x + S(y) = S(x+y)

Since zero is the cardinality of the empty set, it satisfies the property of an additive identity, confirming that 0 is the neutral element for addition.

Theorem 2: The empty set is a subset of every set.

Proof: Let A be any arbitrary set. The empty set has no elements, so there are no counterexamples to the statement that every element of ∅ is also an element of A. Therefore, ∅ ⊆ A.

Theorem 3: There is no largest natural number.

Proof: Suppose there exist a largest natural number, nmax . By the successor function, S(nmax ) must also be a natural number, contradicting the assumption that nmax is the largest. Therefore, no such largest number exists.

The concept of “nothing” is not merely an absence; it is the essential starting point from which all mathematical structures emerge. From the void, we build the numbers, the sets, and the logical systems that underpin modern mathematics. By recognizing the foundational role of “nothing,” we gain deeper insights into the infinite, the structure of numbers, and the very nature of existence within mathematics. The void is, therefore, not just the absence of something but the origin of everything.

In practical applications, the void continues to serve as a useful concept, especially in fields like computer science, where the idea of an empty set is utilized in programming and data structures. The ability to represent and manipulate the void allows for the modelling of complex systems, algorithms, and abstract constructs in various applied disciplines. Its role in shaping both theoretical frameworks and practical models ensures that it will remain central to the development of mathematical and scientific understanding.

1. Kaplan R. The nothing that is: A natural history of zero. Oxford University Press, 1999.

2. Odizilike KN. Lecture notes on Category Theory by Prof. Zurab Janelidze. 2024.

3. The Peano axioms.

4. Enderton HB. A Mathematical Introduction to Logic (2nd ed.). Academic Press. Section 1.4: Truth Tables. 2001; 16-22.