Mechanical Properties Prediction of Hydrogenated Boron Nitride Nanotube
- 1. Department of Nanoengineering, Joint School of Nanscience and Nanoengineering, University of North Carolina, USA
- 2. Nanosciencedepartment, Joint School of Nanscience and Nanoengineering, University of North Carolina, USA
Abstract
Mechanical properties of Hydrogenated Boron Nitride Nanotubes (HBNNTs) were predicted using Molecular Dynamic (MD) simulations. Five armchair BNNTs with different diameters ranging from 0.542 nm to 5.56 nm were hydrogenated on all Nitrogen atoms in their structures. Energy minimization and geometry optimization were performed. MD simulations were then conducted on HBNNTs using ensemble NVT (fixed number of atom, volume and temperature) and NPT (fixed number of atom, pressure and temperature). The Young`s Modulus was obtained using a linear regression to extrapolate the data to the theoretical density of the tubes. MD simulations results show that there is a decrease in Young`s Modulus of BNNTs`when H atomsbonded to all Nitrogen atoms in the system.
Keywords
Boron nitride nanotube , Radiation shielding , Young modulus , Molecular dynamic simulations
Citation
Ghazizadeh M, Estevez JE, Kelkar AD, Ryan JG (2014) Mechanical Properties Prediction of Hydrogenated Boron Nitride Nanotube’s Using Molecular Dynamic Simulations. JSM Nanotechnol Nanomed 2(2): 1030.
ABBREVIATIONS
BNNT: Boron Nitride Nanotubes; HBNNT: Hydrogenated Boron Nitride Nanotubes; NVT: Fixed Number of Atoms, Volume and Temperature; NPT: Fixed Number of Atoms, Pressure and Temperature
INTRODUCTION
Recently, researches related to boron nitride nanotubes have attracted lot of attention due to their similarity to carbon nanotubes (CNTs) [1]. The only difference in BNNT structure is replacement of carbon atoms with bond length of 0.142 nm with Boron and Nitrogen with bond length of 0.147 nm [2]. As a result of this similarity, the two have demonstrated close mechanical properties with superb Young`s Modulus of around1 TPa (E value up to 5 TPa has been reported) [3-5]. The unique and interesting combinations of properties of CNTs and BNNTs have attracted researchers to develop new applications including radiation shielding materials. Eventually these materials are likely to play a key role for the space transportation including human travel to Mars [6-8]. Hydrogenated BNNTs generally have good radiation shielding capabilities, which makes them attractive as compared to aluminum, boron nitride, liquid hydrogen/water and even polyethylene. The main reason for HBNNTs superior shielding properties is due to the fact that three elements (B, N, H) with high radiation shielding capability are present in the same structure. Boron is the key element associated with the radiation shielding characteristics of BNNT’s because of B10’s large neutron capture cross section, making it effective at capturing harmful neutrons [6]. On the other hand, hydrogen is effective in slowing down neutrons and nitrogen is also a good radiation shielding material. This combination makes it possible to protect structural materials, electronics and astronauts from space radiation which is mainly composed of Solar Particle Events (SPE), Galactic Cosmic Rays (GCR), and Secondary Neutrons [6-8].BNNTs ability to offer both structural strength and radiation shielding capability gives researchers the opportunity to incorporate the nanotubes into conventional composite to improve their mechanical properties and shielding performance. Therefore, understanding Hydrogenated BNNTs mechanical properties can provide valuable information regarding their application in space radiation shielding.
Although since finding CNTs, researchers have achieved important advancement related to experimental methods for evaluation of nanotubes` properties, experimental techniques are expensive and limited. The lack of comprehensive experimental methods which allow researchers to study nanotubes under different conditions has resulted in alternate approaches including computational techniques to predict the fundamental properties. Computational techniques to predict fundamental material properties of ideal and defective structures under different conditions has attracted numerous researchers to study physical, thermal, electrical and mechanical properties of different nanotubes including CNTs [9-14], BNNTs [15-20], Aluminum Nitride Nanotubes [19,21] and Titanium Dioxide Nanotubes [20,22-24]. Although computational approach in general provides better flexibility in terms of ability in changing tests conditions, it is very important to approach the problem systematically. Therefore, the present study was divided into two parts; first finding proper simulation parameters and setup which led to acceptable results followed by MD final simulations to determine the Young`s Modulus of hydrogenated BNNT. In order to achieve the first goal, two force fields were selected; Universal and Dreiding as potential candidates [25-27]. Different values of computational steps were investigated in order to find the values between the long and reliable simulations and short and inconsistent one. These molecular dynamics simulations provide a fundamental understanding of the effect of adding Hydrogen to Nitrogen atoms (which is close to 4 atomic weight percentage)of armchair Boron Nitride Nanotubes and to predict associate properties like Young`s Modulus which are generally difficult to measure experimentally.
METHODOLOGY
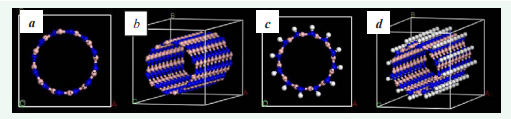
The initial structure of Boron Nitride Nanotubes was modified by bonding Hydrogen atoms to all Nitrogen atoms (Figure 1).
Figure 1 (a-b) (6,6) Nanotube, cross section and side view; C-d) Hydrogenated (6,6) Nanotube, cross section and side view.
In order to design an effective and efficient simulation, two force fields, three energy minimization steps, and three NPT time steps were chosen and best parameters were adopted in the final simulations and are presented in (Table 1).
Table 1: Initial setup considered for obtaining most effective and efficient setup (the chosen setup is in Bold and Italic font).
| Force field | Universal | Dreiding | |
| Minimization Steps | 0 | 500 | 10,000 |
| NPT | 10 ps | 50 ps | 100 ps |
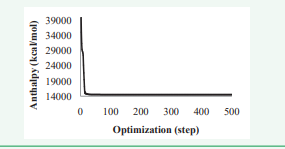
Two different force fields were tested for their consistency and accuracy in conducting simulations. Out of these two force fields, Universal force field was chosen for the final simulations. The geometry optimization was conducted using Smart algorithm and 2.0e-5 kcal/molas cut off value for the energy. Based on obtained data, the simulations indicated that approximately 500 iterative steps were adequate for the HBNNTs simulations (Figure 2).
Figure 2 Energy changes during geometry optimization process of (6, 6) HBNNT.
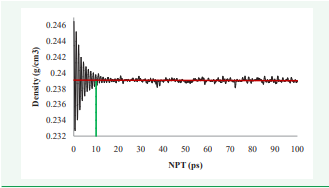
Molecular Dynamic ensemble was conducted for 10,50 and 100 ps while energy and density changes were used for the verification of structure stability. Figure 3
Figure 3 Density changes during NPT simulation for (41,41) HBNNT.
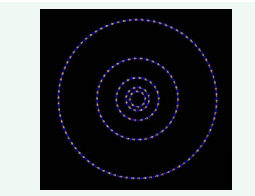
shows the density changes for 100 ps NPT where red line indicates the average value of density (10 ps was chosen for final simulation – green line). Once the simulation setup is finalized, the linear regression technique was used to predict the Young`s Modulus of BNNTs and HBNNTs [14, 16-17].In a nutshell, when the box around nanotubes is in size associated with its theoretical density, the structure collapses during geometry optimization. In order to avoid the structural instability, larger box sizes are employed (in this study, at least four different sizes were used) and Young`s Modulus is then extrapolated to the theoretical density of the material. Five single-walled armchair BNNTs were chosen with different diameters ranging from 0.542 to 5.56 nm including (4, 4), (6, 6), (11, 11), (21, 21) and (41, 41) (Figure 4).
Figure 4 BNNTs used for simulation; (4,4) with diameter of 0.542 nm, (6,6) with diameter of 0.814 nm, (11,11) with diameter of 1.492 nm, (21,21) with diameter of 2.848 nm and (41,41) with diameter of 5.56 nm.
The summary of the analysis parameters that were used in MD simulations for the various BNNTs and HBNNTs were:
• Cell size: The lattice size in x and y is different for each tube while z remained constant (---x---x24.6) ?, and lattice angles are (α = 90, β = 90, γ = 90).
• Force field: Universal.
• Energy minimization: Smart minimization, 500 step.
MD ensemble: NVT and NPT.
MD ensemble: NVT and NPT.
Temperature control: Anderson.
Pressure values: atmospheric
Pressure control: Berendsen
Time step: 1.0 femto second (fs).
Dynamics time: 10 pico second (ps)
RESULTS AND DISCUSSION
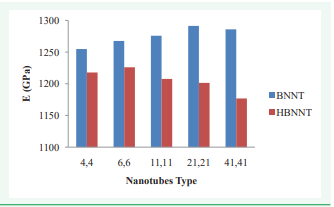
The Young’s Modulus of (4, 4), (6, 6), (11, 11), (21, 21) and (41, 41) BNNTs and HBNNTs were determined using the extrapolation technique as explained before (Figures 5, 6).
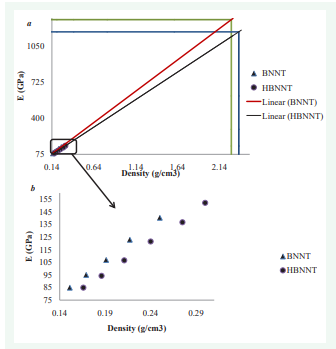
Figure 5 a) Extrapolation technique used for prediction of E value for (41,41) BNNT and HBNNT where black line shows linear regression for HBNNT, red line shows linear regression for BNNT, blue lines show HBNNT`s Young`s Modulus at density value of 2.37 g/cm3 and green lines show BNNT`s Young`s Modulus at theoretical density of 2.28 g/cm3; © b) Actual E values obtained for different cell sizes for (41, 41) BNNT and HBNNT.
Figure 6
Figure 6 Predicted Young`s Modulus for all five BNNTs and HBNNTs.
Young`s Moduli values were predicted based upon the theoretical density of 2.28 g/cm3 for BNNTs while the density value used for HBNNTs was slightly higher due to the presence of hydrogen atoms and was set at 2.37 g/cm3 . Figure 5 shows the extrapolation technique used for (41, 41) BNNT and HBNNT where Young`s Modulus of 1286 and 1177 GPa were predicted, respectively. Figure 6 shows predicted value of Young`s Modulus for all the ten different nanotube configurations. The molecular dynamics simulations indicate that all nanotubes show less Young`s Modulus once Hydrogen atoms were added to the structure. The decrease in value of E ranges between 2.94, 3.28, 5.34, 6.96 and 8.48 percent for nanotubes with chirality of (4, 4), (6, 6), (11, 11), (21, 21) and (41, 41), respectively.
Although, based on predicted data, adding hydrogen atoms to nitrogen atoms in the structure of BNNT results in decrease of the elastic modulus and degradation of mechanical properties, HBNNTs still offer a unique and interesting combination of strength and shielding capability. Therefore, if fabrication challenges are overcome and good quality composites are fabricated by dispersing HBNNTs, addition of Boron Nitride nanotubes are expected to increase the mechanical strength of carbon fiber reinforced nanocomposites while improving chemical and thermal stability and radiation shielding capability.
CONCLUSIONS
In present work, effects of bonding hydrogen atoms to nitrogen atoms in the structure of armchair BNNTs was investigated. The results indicate that adding almost 4 atomic weight percentage of H to the BNNT will result in Young`s Modulus degradation but the amount of decrease in the modulus values is also dependent upon diameter of the nanotubes. The maximum degradation of 8.5% was seen in (41, 41) HBNNTs with 5.56 nm diameter. Although adding H to the structure of BNNT has resulted in some degree of degradation, the modulus of HBNNTs is still much higher than the current best counterpart like carbon fibers which indicates that addition of HBNNTs to conventional carbon fiber reinforced polymeric composite system will have superior mechanical and radiation shielding capabilities as compared to convention carbon fiber reinforced polymeric composites and the HBNNT infused material will be an excellent candidate for future space structural applications.