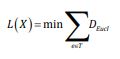Intrinsic Dimensionality Estimation in Visualizing Toxicity Data
- 1. Frumkin Institute of Physical Chemistry & Electrochemistry, Russian Academy of Sciences, Russia
- 2. Moscow Institute of Physics & Technology, Russian Academy of Sciences, Russia
Abstract
Over the years, a number of dimensionality reduction techniques have been proposed and used in chemo informatics to perform nonlinear mappings. Nevertheless, data visualization techniques can be efficiently applied for dimensionality reduction mainly in a case if the data are not really high-dimensional and can be represented as a nonlinear low-dimensional manifold when it is possible to reduce dimensionality without significant information loss. In this study several intrinsic dimensionality estimation approaches have been investigated: the Geodesic Minimum Spanning Tree, the Eigen value-based and the Maximum Likelihood Estimators. Their performance has been compared for visualizing toxicity data in different descriptor spaces.
Keywords
• Chemography
• Chemoinformatics
• Dimensionality reduction
• Intrinsic dimensionality estimators
• Drug design
• Toxicity
• Geodesic minimum spanning tree
• Maximum likelihood estimators
Citation
Kireeva N, Ovchinnikova SI, Tsivadze AY (2014) Intrinsic Dimensionality Estimation in Visualizing Toxicity Data. J Drug Des Res 1(1): 1002.
INTRODUCTION
Over the years, a number of dimensionality reduction techniques have been proposed and used in chemo informatics to perform nonlinear mappings. Nevertheless, data visualization techniques can be efficiently applied for dimensionality reduction mainly in a case if the data are not really high-dimensional and can be represented as a nonlinear low-dimensional manifold when it is possible to reduce dimensionality without significant information loss [1]. In this study several intrinsic dimensionality estimation [2] approaches have been investigated: the Geodesic Minimum Spanning Tree [3], the Eigen value-based [4,5] and the Maximum Likelihood Estimators [1]. Their performance has been compared for visualizing toxicity data in different descriptor spaces. The obtained values of data intrinsic dimensionality (ID) were compared with the quantitative results of data visualization for two applied dimensionality reduction approaches: Diffusion maps and Isomap.
MATERIALS AND METHODS
For intrinsic dimensionality estimation and dimensionality reduction the implementations provided by Matlab Toolbox for Dimensionality Reduction (v 0.7.1b) [6] were used.
Intrinsic dimensionality estimators
The intrinsic dimensionality of the data can be defined as the minimal number of variables needed to describe the data x. The intrinsic dimensionality estimators can be related to two main categories: the eigen value or projection methods and the geometric methods. Eigen value methods are based on principal component analysis (PCA) [7]. PCA projects the data along the directions of maximal variance. It computes eigen values and eigenvectors of the covariance matrix of data. Intrinsic Dimensionality (ID) is defined by the number of eigen values that exceed a predefined value of threshold. The geometric methods are mostly based on fractal dimensions or nearest neighbor distances. In this study, the Geodesic Minimum Spanning Tree [3] and Maximum Likelihood Estimator [1] were used as representatives of second group of methods.
In Geodesic Minimum Spanning Tree (GMST) several steps are considered. First, a complete graph based on geodesic distances between all pairs of data points is built. A minimal spanning graph, or the GMST, is obtained by the reduction of the initial graph to a subgraph, in which every data point xi is connected to its k nearest neighbors. The intrinsic dimension is estimated from the GMST length functional L:
where T is the set of all sub-trees of graph G, e is an edge in tree T, and DEucl is the Euclidean distance corresponding to the edge e.
Maximum Likelihood Estimator is based on number of data points covered by a hypersphere with a increasing radius by modeling the number of data points inside the hypersphere as a homogeneous Poisson process. In practice the radius is usually replaced by the number of neighbors k. Since this parameter impacts the estimation of ID, here, we use the average value of ID defined in the range of k (see details below). ID value is estimated maximizing log-likelihood of the Poisson process.
Dimensionality reduction approaches
In this study, two representatives of distance-preserving nonlinear dimensionality reduction methods Isomap (IM) [8,9] and Diffusion Maps (DM) [10] are used. This group of techniques is intended to use distance preservation as the criterion for dimensionality reduction that is intuitively understandable and easy to compute.
Assessment of data visualization performance
The performance of data visualization has been monitored with quantitative measure introduced and proved its efficiency in [11] and which is an average value of two other parameters, DC and DSC, that reflect different features of the visualization maps and thus are complementary to each other [11].
Data preparation
Three data sets were considered in this study. A set of 242 pIC50 values for hERG inhibition was taken from [12]. To generate the classification models the considered data set was split into two classes according to their activities on the hERG channel inhibition. The pIC50 = 5 (low micromolar potency) was considered as the threshold value for hERG inhibition. Thus, 104 inactive and 138 active compounds for hERG channel inhibition have been involved in model development.
A set of 100 phospholipidosis-inducing compounds and 82 negative drug like compounds were taken from [13], where the active compounds have been observed to act on a range of species (humans, rats, mice, dogs, rabbits, hamsters and monkeys) and on a variety of tissue types (lungs, kidney and liver).
Data from EPA Fathead Minnow Acute Toxicity Database [14] after data preparation stage containing 612compounds. This database was generated by the U.S. EPA Mid-Continental Ecology Division (MED) for the purpose of developing an expert system to predict acute toxicity from chemical structures based on mode of action considerations. A threshold of 1mmol/L was used to subdivide compounds on toxic and non-toxic. After removal of several compounds with activities identified as ranges, the final dataset included 578 compounds (145 non-toxic and 433 toxic).
The data preparation has been carried out using recommendations published in [15]. Chemaxon Standardizer [16] and Instant JChem [17] software have been used for the data preparation. Using Standardizer, the explicit hydrogen atoms have been removed, the structures have been aromatized.
Descriptors
In this study, four descriptor types were involved in model development. ISIDA package [18] was represented by two different descriptor types: (i) ISIDA Property-Labeled Fragment Descriptors (IPLF)[19] (atom-centered fragments (augmented atoms) of radius 1 to 3 colored by pH-dependent pharmacophores and (ii) subclass of ISIDA Substructural Molecular Fragments (SMF)[18] consisting of the shortest topological paths with explicit representation of only terminal atoms and bonds, where the values of minimal nmin and maximal nmax number of atoms varied from 2 to 15. 2D descriptors of Molecular Operating Environment (MOE 2D)[20] containing different physical properties, subdivided surface areas, atom and bond counts, Kier & Hall connectivity and Kappa shape indices, adjacency and distance matrix descriptors, pharmacophore feature descriptors and partial charge descriptors were involved in model development. Finally, 2D descriptors calculated with Dragon v 6.0 software [21] were used.
Computational procedures
GMST. It was found that the results obtained with GMST are highly dependent on random parameters and therefore for each combination of data set and descriptor type we used an average of 300 estimates. k = 50 nearest neighbors were used to construct a connectivity graph, M = 3. N = 30 random permutations were used to sum the cumulative distance.
EV. The only external parameter required in the Eigenvalues method is the value of a threshold for the eigenvalues. It was set to thr = 0.025.
MLE. The neighborhood range was set from k1 = 10 to k2 = 30.
RESULTS AND DISCUSSION
In this study, Maximum Likelihood Estimation, Geodesic Minimal Spanning Tree and Eigen value method have been applied for intrinsic dimensionality estimation. The obtained values of data intrinsic dimensionality (ID) were compared with the quantitative results of data visualization for the applied dimensionality reduction methods.
Figure 1 The average value of for twenty best maps for each combination of data set and descriptor type (corresponds to a point on the graph). The maps were obtained by DM (I, II), Isomap (III), the intrinsic dimensionality was calculated by MLE (I), GMST (II), EV (III). The points that correspond to the same data set are connected by a dash line.
In Figure 1 (I) the value is represented as a function of the intrinsic dimensionality for each data set (each point represents a combination of data set and descriptor type). Here, the inverse relationship between the number of intrinsic dimensions and the quality of visualization model is observed. One can see, that the significant decrease in class separation ability
for hERG data set can be explained by the increase in intrinsic dimensionality from 7-8 to 21 (for IPLF descriptors). The similar decrease can be found for acute toxicity dataset
though the intrinsic dimensionality varies in a smaller range (from 5 to 9). At the same time, the changes of intrinsic dimensionality for phospholipidosis from 5 to 22 have a negligible impact to the considered parameter (from 0.75 to 0.72).
Figures 1 (II) and 1 (III) demonstrate the same regularities for GMST and EV methods of estimation of intrinsic dimensionality. One can see, that for GMST dimensionality of data enough confidently associated with the performance of obtained maps whereas for phospholipidosis increasing the number of intrinsic dimensions has no impact on visualization quality.
Eigen values defines the number of intrinsic dimensionalities different from those, produced by MLE and GMST. The combination of this approach with DM was unable to find the same trend.
According to GMST the intrinsic dimensionality of considered data sets varied in a larger range (up to 96 for herg, IPLF descriptors) then according to MLE (up to 22 for phospholipidosis, IPLF descriptors). The same value for EV is even smaller: the largest value intrinsic dimensionality among all considered datasets was, according to this method, 9. This makes it impossible to exactly assess the real value of intrinsic dimensionality, but we still can make some tentative conclusions by comparing the relative values to each other. The disagreement of the obtained by different ID estimators results required a further comprehensive study.
Among the three studied algorithms, Maximum Likelihood Estimation, Geodesic Minimal Spanning Tree and Eigen value method, the MLE demonstrated to be the most efficient one, since its results better correspond to the obtained visualization maps.
CONCLUSION
In this study several intrinsic dimensionality estimation approaches have been investigated: the Geodesic Minimum Spanning Tree, the Eigen value-based and the Maximum Likelihood Estimators. Their performance has been compared for visualizing toxicity data in different descriptor spaces. Among the studied algorithms the MLE demonstrated to be the most efficient one, since its results better correspond to the obtained visualization maps. The disagreement of the obtained by different ID estimators results required a further comprehensive study.
ACKNOWLEDGEMENTS
Authors thank Russian Foundation for Basic Research (projects no. 11-03-00161 and 12-03-33086) for the support.
REFERENCES
7. Jolliffe IT. Principal Component Analysis. Springer series in statistics. New York: Springer, 2002.
10. Coifman RR, Lafon Sp. Diffusion maps. Applied and Computational Harmonic Analysis. 2006; 21: 5-30.
16. Chemaxon Standardizer. http://www.chemaxon.com/library/ scientific-presentations/standardizer/.
17. Instant JChem; www.chemaxon.com/products/instant-jchem/.
20. Instant JChem. Available from URL: www.chemaxon.com/products/ instant-jchem/