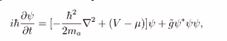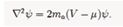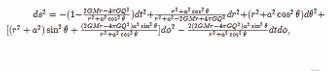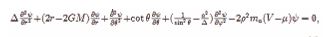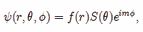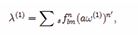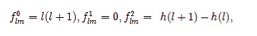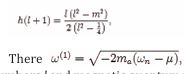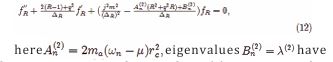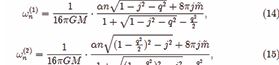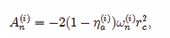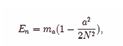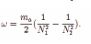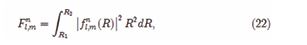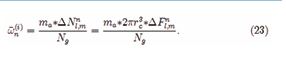The superfluid axion equations on the rotating black hole background are derived in this paper. When axions absorb the energy of gravitational wave radiation from the quantized black holes, then these axions can form the different energy levels and vortex states. We calculated the particle number densities and total mass of axions around Kerr-Newman and Kerr-Sen black holes. Moreover, the gravitational wave radiation frequencies of superfluid axions are also calculated in the different energy levels and vortex states.

• Gravitational Wave

• Black Hole

• Axion

• Dark Matter

Chen YA, Yu Y, Zhao F, Yan J (2025) Gravitational Wave Radiation from Superfluid Axions around the Quantum Black Holes. J Phys Appl and Mech 2(1): 1010.

In order to resolve the strong CP problem in QCD theory, Peccei and Quinn postulated a new spontaneous breaking of global U(1) symmetry [1]. Subsequently, Weinberg and Wilczek pointed out that this fact would lead to the existence of a new particle [2-3], this light neutral boson was called axion. Preskill and Abbott et al, discussed the application of axion in cosmology by the improving mechanism [4-6]. Axion is one candidate of the dark matter, and it may produce in the QCD transition at early universe. The axion field energy density decreases with the expansion of the universe, when the cosmic temperature is reduced to a certain temperature, then the hot axions will evolve to the cold axions in the late universe, which can form Bose-Einstein condensate in various forms.Axion also plays a special role in string theory, this superlight axion can be used as a new probe tool to test string theory. Svr?cek and Witten recalculated the relation of axion mass m and decay constant fa and they found m to depend on the mass of quarks u, d and pion [7]. Moreover, the decay constant fa can be derived from string effective action, the magnitude of fa is above 1016 ∼ 1017 GeV and it very close to the GUT scale. This means that allowed to exist a very light axion (10-10 eV), and the mass of QCD axion with high energy breaking scale can match the mass of stellar mass black hole.Arvanitaki et al., discussed some observational effects of axions around a astrophysical black hole [8-10], when Compton wavelength of axion matches with the Schwarzschild radius of a black hole, the axion cloud can form superradiant bound states through extracting black hole mass and angular momentum. Here, the amplified mechanism of axion field play a key role to produce an exponentially growing bound states, these unstable axions may emit gravitational waves from different energy levels transitions. Moreover, Mocanu and Grumiller analysed collapse process of axion cloud according to particle number change and self-organized criticality [11], they found that nonlinear interaction of the bosons could cause the sudden collapse of axion cloud and bring out some Bose-nova explosion, this event can also release axion energy and engenders the gravitational wave radiant effect. Yoshino and Kodama also studied the nonlinear character of Bose field and numerically simulated the collapse process of axion, their research showed that Bose- nova can happen and this phenomenon is the result of the superradiance instability [12-13].Mielczarek et al analyzed BEC condensation of axions on the galactic scale [14], they used an analytical method for explaining the shapes of galaxy rotation curves, and found the axion mass can impact on the dark matter composition way. Only ultralight axions can form large scale structures, but relatively light axions will constitute small scales matter structures. In additional, quantum vortexes in superfluid axions have a unique property, that they can distinguish different types of dark matter, the rotation of condensed matter is a fountainhead of vortex occurrence [15-16]. Meanwhile, the axion vortexes may also generate primordial angular momenta of early galaxies. In the previous work, we have studied the density distribution of BEC axions on the different black hole backgrounds [17], and discussed the impact of chemical potential µ to the axion density. We found that µ > 0 describes a high density superfluid state, and µ < 0 is corresponding to a low density normal state. In this paper, we will study the axion density distribution around the quantum black holes, those axions can exist in the form of superfluid state with vortex structure. When axions absorb the energy of gravitational waves from black hole radiation, then the axion density will increase and occur transitions from high energy level to low energy level. At the same time, axions will radiate gravitational waves again. Moreover, with the rise of temperature, axions will undergo a phase transition from superfluid state to normal state. In this process the axion’s particle density will have a great change and lead to axion radiate gravitational waves too.

Superfluid axion equations on the rotating black hole background

We assumed that axions can produce BEC condensation around a black hole, then motion equation of the axions can be expressed by the following Gross-Pitaevskill equation (GPE) in the curved space-time

where the mass of axion is are the axion wave functions, V (r) is the interaction potential, µ represent the chemical potential, g˜ is the coupling constant. For the weak coupling axions, we can ignore the nonlinear term. If the wave function will not change with time, then the metric g is time- independent, after taking the nature units, then the static GPE will become

In atomic physics, V (r) in the G-P equation is taken to be an external harmonic trapping potential, mean-field self interactions can also be described by V (r). In general case, this potential term cannot allowed transition frequencies of the system, but for an electron-phonon system in a quantizing magnetic field, the energy spectrum is discrete and it can be expressed by the quantum number n of the Landu level [18]. From the point of view of quantum theory, electrons absorb the energy of electric field, which is equivalent to realizing the transition of electrons between Landau energy levels. Moreover, in the spinor BEC model, there is the Zeeman energy En shift caused by the constant magnetic field, where the quantum number n =1,0,-1 means that the atom is in different energy levels, and the particle numbers on the three energy levels are also different [19,20]. In this paper, since the radiation frequencies ωn of gravitational wave depend on the quantum number n of area change, and the frequencies ωn are similar to the constant Zeeman energy shift, so the wave function and particle number are related to the quantum number n, the distribution of axion number in each energy level is different. In this case, when the axions absorb the energy of the gravitational wave from the black hole, they can form different energy levels and the transition process can produce.The axions interaction is very weak in the early universe, their typical initial wavenumber is about  where is the Hubble parameter at the QCD phase transition [21], so the axions are highly non- relativistic after phase transition. In addition, the speed of the axions in a galaxy can be expressed as , is the observation distance of the galaxy [14]. When typical observed value is taken as R0=10hps , axion mass is ma =10—10eV, 

, then we got the speed Va10—7 m/s. Therefore,

the speed of the axions in the galaxy is very low, the non-relativistic G-P equation (2) can be used to describe the motion of light scalar particles in the astrophysical environment [22], so linear G-P equation (2) becomes the start point of our following studying. The distribution of axions around different black holes can be determined by different form metric g, we will calculate and compare the particle number densities and gravitational wave frequencies of the axions in the Kerr-Newman black hole and the Kerr-Sen black hole backgrounds.

The Kerr-Newman metric can be written as

where M is the mass of black hole, a = J/M , J is the spin angular momentum, Q is the charge. Substituting the metric (3) into Eq.(2), we obtain the wave function equation

where V = ωn are radiation frequencies of gravitational wave, ? = r2 + a2 + 4GQ2-2GMr and ρ2 = r2 +a2 cos2 , the form of this equation is similar to Teukolsky equation [23], but the physical meaning is different, this equation describes the non-relativistic motion of the axions around a rotating black hole.

We take the axion wave function ψ as

Eq.(4) can be separated to two equations

where λ(1) is the eigenvalues of spin-weighted spheroidal functions [24,25] and it has the following expansion formula

when spin  = 0, the low order coefficients are

where

the angular quantum numbers l and magnetic quantum numbers m can describe the vortex structures of the BEC axions. If axions form vortex states around some black holes, then these excited vortexes are corresponding to different axion densities. Let us define GM = rc , then radial equation can be taken as the following form through the coordinate transformation

For certain mass black hole, the radiation frequencies ωn and chemical potential µ are the main factors to influence the density distribution of axions. Moreover, the eigenvalues depended on the angular momentum a and parameter ω(1). The Kerr-Sen metric in string theory can be expressed as [26]

and m¯ = GM — 2πGQ2/M . To repeat the same derivation in K-N metric we can get the similar radial equation

the same expansion form with Eq.(8). Comparing this equation with Eq.(10), we can see that the only difference is the charge term q2, this means that the density distribution law of axion is different on the K-N black hole background and K-S black hole background. In next section, we will apply these equations to study the axion’s gravitational wave radiation process around the rotating black holes.

The axion’s gravitational wave radiation process

It is well-known that the entropy of the black hole is proportional to its horizon area. In order to explain this exotic feature, Bekenstein and Mukhanov proposed that the area A of black hole horizons is quantized by units of the Planck area [27,28]

 

where α is a dimensionless coefficient for certain black hole, and N is an integer. The value of α can be calculated in the different methods. Bekenstein and Makhanov obtained a analytic result α = 4lnq for the Schwarschild black hole through a statistical physical approach [29]. Forthermore, Hod get a value α = 4ln3 from the real part of the Quasinormal Modes (QNM) frequencies and Bohr’s Correspondence Principle [30]. Kunstatter recalculated this parameter by using the adiabatic invariant method [31]. Maggionre pointed out that the QNM behavior is similar to a damped harmonic oscillators and classical frequencies relate to both real and complex parts of QNM, so the coefficient should be modified as α = 8[32]. Vagenas studied the area spectrum of Kerr black hole [33] and Medved found that when J M 2 the value α = 8 can be derived from a general adiabatic invariant [34]. For K-N and K-S black holes, if the ratio of charge and mass is a small quantity, The correct formula in the sentence α = 8  by using a similar adiabatic invariant.

Foit and Kleban calculated the radiated frequencies of graviton for a quantum Kerr black hole [35], they pointed out the Bekenstein-Makhanov hypothesis may be tested from the QNM frequencies in the rings down phase of binary merger. For Kerr-Newman black hole or Kerr-Sen black hole, the change of the area ?A are accompanied by a change of quantum number n = -?N . So according to the relationship

, we separately obtain the follow quantum frequencies

where  magnetic

quantum numbers. The radiated frequency of K-S black hole have a similar form with K-N black hole and the otherness only reflected in the q charge term.

When axion clouds absorb the radiated energy of rotating black holes, the radiation frequencies can be written as  where  are corresponding to the radiated frequencies of K-N and K-S black holes, respectively describes the normal state or superfluid state of axion matter [36].

Total particle number of axions can be rewritten in the R coordinate

Numerical Calculation Results

LIGO and VIGO collaboration have observed a series of gravitational wave signals after the merger of two black holes [37-41]. Their reports showed that the mass of final black hole are between  times sun mass and  times sun mass , and the spin of final black hole are between  and . So in order to get the numerical solutions of Eq.(10) and Eq.(12), we choose the physical parameters as follow: the mass of black hole is 30 times sun mass, the spin and charge are j = 0.720 and q = 0.697, meanwhile j2 + q2»1, we take the mass of axion m

= 10  eV, so the gravitational wave absorbance coefficient

 can be represented as

where  and the other parameter  are the eigenvalues of spin-weighted spheroidal functions

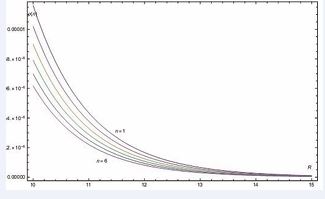
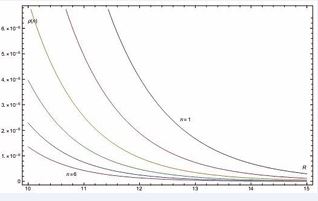
For the K-N and K-S black hole, when                the axions are in the normal state, we let       and take integral interval from  the particles number density  in different energy levels and without vortex excitation, are shown in Figure 1 and Figure 2. So it is obviously to see that particles number density will decrease when energy levels from n = 1 change into n = 6, this means that the spontaneous transition process cannot occur in the axion’s normal state. Moreover, the calculation results showed that the densities are smooth decay outside the horizon and axions can form bound states around K-N and K-S black holes. When  axions are in the superfluid state and

Figure 1: In the normal state, the axion number densities around K-N black hole with different energy level.

Figure 2: In the normal state, the axion number densities around K-S black hole with different energy level

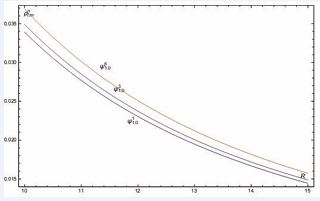
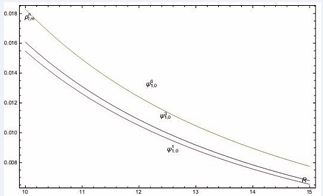
they will emerge vortex distribution. Let us take

energy levels and different vortex states. We choose the quantum number l = 1, m = 0 to compare the particle number densities in the different energy levels, the calculation results are shown in Figure 3 and Figure 4. When the vortex quantum numbers are the same, then high energy level correspond to more particles, and spontaneous transition process can happen. Superfluid axions can also form bound state around K-N and K-S black holes, it is worth mentioning that the superfluid axion’s numbers are far more then the normal state axion’s numbers. For the K-S black hole, the radial equation of axion wave function has the similar form with K-N black hole, but the charge term is different, this difference lead to the change of axion density, so the axion’s densities around K-N black hole are larger than the axion’s densities around K-S black hole.

Figure 3: In the superfluid state, the axion number densities around K-N black hole with same vortex number but different energy level.

Figure 4: In the superfluid state, the axion number densities around K-S black hole with same vortex number but different energy level.

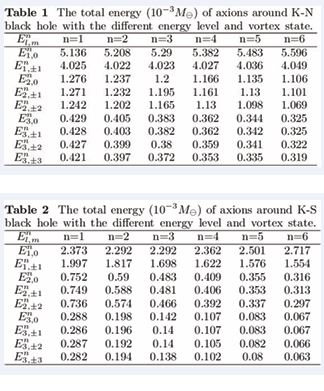
When  we can calculate the total energy of axions on each excitation state, here energy level distribution are n = 1 to n = 6 and vortex quantum number distribution are l = 1 to l = 3, the calculation results are shown in Table 1 and Table 2. The unit of energy is 10-3 times of the moon mass , the magnitude of total particle number close to 1068, this number will determined by the mass of the axion. The energy of high energy level with low vortex states are more then the energy of low energy level with high vortex state  which means that the spontaneous transition process can just happen at the low vortex states. In addition, the total energy of axions around the K-N black hole is greater then the total energy of axions around the K-S black hole.

Arvanitaki et.al studied the energy spectrum of the superradiant axion cloud around the rotating black hole[9], they found the quantized energy levels are very similar to the energy levels of a hydrogen atom. Accordingto the discussion of Arvanitaki et.al, the superradiant energy level of axions can be expressed as

where, a = ma rc , N = n + l + 1 is the principal quantum number, l is is the orbital angular momentum, so the difference between two different energy levels represents the radiation frequency of the axions, that is

In order to calculate the frequencies of emitted gravitons from 6g to 5g state, we take principal quantum number as N1 = 5, N2 = 6, when a = 1, we have

when a = 2, then we get  these

frequencies of emitted gravitons close to the low frequency part of our following calculation results. Now we can calculate the gravitational wave radiation frequency of the superfluid axions. In general case, the spontaneous transition process will accompany with the emission of gravitational wave, thus the particle number function  is defined as

the gravitational wave radiation frequencies in the different black hole background can be expressed as

  are  the  particle  number  difference 

of different energy levels and vortex states,  is the number of emitted gravitons, ε is a dimension less constant. Here, the transition energy  has been converted into the gravitational wave radiation energy , the numerical calculation results show that particle number difference . When we take = 108, from Eq.(23) we can get the radiation frequency relation , so the frequencies of the gravitational wave be calculated by energy level difference

(21) is also within the range of this radiation frequency. In the following calculation we will take then the

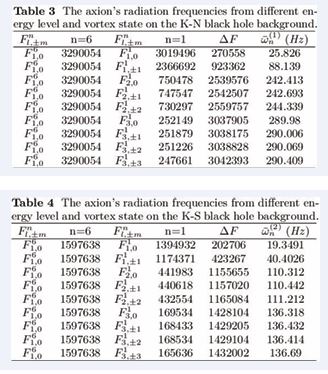
axion radiation frequencies from n = 6 to n = 1 are shown in Table 3 and Table 4. When η(i) is certain, we can see that the radiation frequencies in high vortex numbers are more than the radiation frequencies in low vortex numbers, the particle numbers around K-N black hole background are more than they around K-S black hole background. In addition, the axion’s radiation frequencies on the K-S black hole background are less than the axion’s radiation frequencies on the K-N black hole background. 

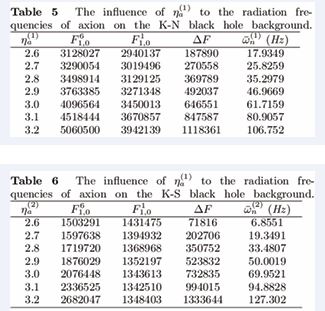
When  changes, from Table 5 and Table 6, it is easy to see that the gravitational wave radiation frequencies increase with  increase. If  takes 2.6 to 2.8, every radiation frequency of axions on the K-N black hole background is more than that on the K-S black hole background. If  takes 2.9 to 3.2, every radiation frequency of axions on the K-N black hole background is less than that on the K-S black hole background. So the change of  will have an important impact to the radiation frequencies

of the gravitational wave. Since the supermassive black hole merge process can also emit the low frequency gravitational wave signal, Will et.al suggested that use the LISA detector to observe the ringdown waveform of massive black holes merge [42].

The combined process of black holes can radiate gravitational waves, when this merger of two-black holes is finished, the area of the black hole will decrease, the mass and angular momentum will also decrease. Moreover, the energy of gravitational wave will be absorbed by the axion matter around the black holes, these axions can form in different energy levels and vortex states. In this paper we studied the axion number distributed law on the Kerr- Newman and Kerr-Sen black hole background. At the same time, we also calculated the gravitational wave radiation frequencies and found the following fact:

(1) In the normal state or superfluid state, the axions densities are decay outside the horizon and axions can form bound states around K-N black holes or K-S black holes.

(2) In the normal state, the spontaneous transition process cannot be occur, but in the superfluid state the spontaneous transition can happen.

(3) We found that the total energy of axions on the K-N black hole background is greater than the total energy of axions on the K-S black hole background, the axion spontaneous transition process can happen at the low vortex states.

(4) We separately calculated the gravitational wave 

radiation frequencies of axions around two types of black holes, if the  parameters are certain, the calculation results showed that the axion’s frequencies on the K-S black hole background are less than the axion’s frequencies on the K-N black hole background. The magnitude of these frequencies is about 5Hz to 300Hz. Moreover, the change of  parameters will bring a obvious impact to the radiation frequency. When the radiation process of superfiuld axions is completed, the numbers of particle will be greatly reduced. This may occur the phase transition from the superfiuld state to the normal state, the gravitational waves radiation of the axions will stop with the phase transition to finish.

We hope that the results of this study may provide an alternative physical mechanism to explain the gravitational wave radiation of the axions.

1. R.D.Peccei and H.R. Quinn. Constraints imposed by CP conservation in the presence of pesudo-particles. Phys. Rev. D 16, 1791(1997).
2. S.Weinberg, A new light boson? Phys. Rev. Lett. 40, 223(1978).
3. F.Wilczek, Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 40, 279(1978).
4. J.Preskill, M.B. Wise and F. Wilczek, Cosmology of the invisible axion. Phys. Lett. B. 1983; 120, 127(1983).
5. L.F.Abbott and P. Sikivie, A cosmological bound on the invisible axion. Phys. Lett. B. 1983; 120, 133(1983).
6. P.Sikivie, Axion cosmology. Lect. Notes. Phys. 741, 19(2006).
7. P.Sv?ccek and E. Witten, Axions in string theory. J. High. Energy. Phys.0606, 573(2006).
8. A.Arvanitaki, S. Dimopoulos, and S. Dubovsky et.al String axiverse Phys. Rev. D. 81, 95(2009).
9. A.Arvanitaki and S Dubovsky. Exploring the string axiverse with preci- sion black hole physics. Phys. Rev. D. 83, 337(2012).
10. A.Arvanitaki, M. Baryakhtar, and X. Huang, Discovering the QCD ax- ion with black holes and gravitational waves. Phys. Rev. D. 91, 084011(2016).
11. G.R.Mocanu and D. Grumiller, Self-organized criticality in boson clouds around black holes. Phys. Rev. D. 85, 96(2012).
12. H.Yoshino and H. Kodama, Bosenova collapse of axion cloud around a rotating black hole. Prog. Theor. Phys. 128, 153(2012).
13. H.Yoshino and H Kodama, Bosenova and axiverse. Class. Quantum Grav. 32, 214001(2015).
14. J.Mielczarek, T. Stachowiak, and M. Szydowski, Vortex in axion conden- sate as a dark matter halo. Int. J. Mod. Phys. D. 11, 1843(2010).
15. T.Harko and E. Madarassy, Finite temperature effects in Bose-Einstein condensed dark matter halos. JCAP. 2012, 020(2012).
16. C.G.Boehmer, T. Harko, Can dark matter be a Bose-Einstein con- densate? JCAP. 025(2007)
17. J.Yan. The density distribution of axion matter on the black hole back- ground Sci. China Phys. Mech. 45, 090001(2015). (in Chinese)
18. V.N.Popov, Low frequency asymptotic behavior of the phonon Green function and kinetic equations for an electron-phonon system in a quantizing magnetic field. JETP. 33, 127(1971).
19. L.Chang, Q. Zhai, R. Lu, and L You. Number fluctuation dynamics of atomic spin mixing inside a condensate. Phys. Rev. Lett. 99, 080402(2007).
20. Q.Zhai, L Chang, R Lu, L You. Number fluctuation dynamics of a spin-1atomic condensate. Phys. Rev.A.79, 043608(2009).
21. A.H.Guth, M.P. Hertzberg, and C.P. Weinstein, Do dark matter axions form a condensate with long-range correlation. Phys. Rev. D. 92, 103513(2015).
22. L.Hui, J.P. Ostriker, S.Tremaine, and E.Witten, Ultralight scalars as cosmological dark matter. Phys. Rev. D. 95, 043541(2017).
23. S.A.Teukolsky, Rotating black holes: separable wave equations for gravitational and electromagnetic perturbations. Phys. Rev. Lett. 29, 1114(1972).
24. E.Seidel, A comment on the eigenvalues of spin-weighted spheroidal functions Class. Quantum Grav. 6, 1057(1988).
25. E.Berti. Eigenvalues and eigenfunctions of spin-weighted spheroidal harmonics in four and higher dimensions. Phys. Rev. D. 73, 1111(2005).
26. A.Sen, Rotating charged black hole solution in heterotic string theory. Phys. Rev. Lett. 69, 1006(1992).
27. J.D.Bekenstein, The quantum mass spectrum of the Kerr black hole. Lett. Nuovo Cimento. 1974; 11: 467(1974).
28. V.F.Mukhanov, Are black holes quantized? JETP.Lett. 44, 63(1987).
29. J.D.Bekenstein and V.F.Mukhanov, Spectroscopy of the quantum black hole. Phys. Lett. B. 360, 7(1995).
30. S.Hod, Bohr’s correspondence principle and the area spectrum of quan- tum black holes. Phys. Rev. Lett. 81, 4293(1998).
31. G.Kunstatter, d-dimensional black hole entropy spectrum from quasinormal modes. Phys. Rev. Lett. 90, 161301(2003).
32. M.Maggiore, Physical interpretation of the spectrum of black hole quasinormal modes. Phys. Rev. Lett. 100, 141301(2008).
33. E.C.Vagenas, Area spectrum of rotating black holes via the new interpretation of quasinormal modes J. High. Energy Phys. 11, 2379(2008).
34. A.J.Medved, On the Kerr quantum area spectrum Class. Quantum Grav. 25, 2867(2018).
35. V.F.Foit and M Kleban, Testing quantum black holes with gravitational waves. Class. Quantum Grav. 36, 035006(2019).
36. V.N.Popov. Possible failure of the scaling law upon phase transitionof a Bose system to a superfluid state. J. Math. Sci. 46, 1619(1989).
37. B.P.Abbott et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 116, 061102(2016).
38. B.P. Abbott et al. Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016; 241103(2016).
39. B.P. Abbott et al, Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 118, 221101(2017).
40. B.PAbbott et al, Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Astrophys. J. Gett. 851, L35(2017).
41. B.P.Abbott et al, Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 119, 141101(2017).
42. E.Berti, V Cardoso. C.M.Will. On gravitational wave spectroscopy of massive black holes with the space interferometer LISA. Phys. Rev.D. 73: 348(2006).