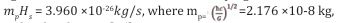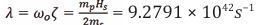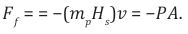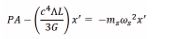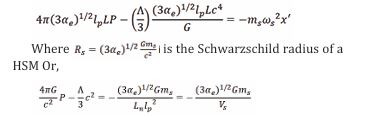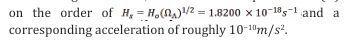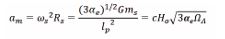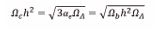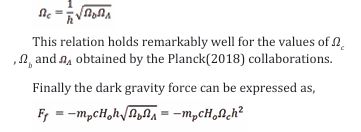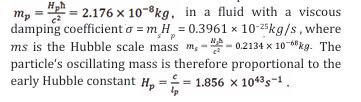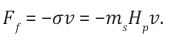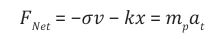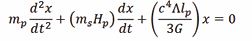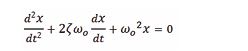On Spacetime as a Damped Harmonic Oscillator and The Dark Universe
- 1. Independent Researcher at Bill Stone Services, Uganda
Abstract
We present the structure of space-time as an oscillating Hubble Scale Mass (HSM) particle in a viscous fluid of Planck mass relics. Due to this particle oscillations and its interaction with a residual Planck mass, spacetime is undergoing a damped harmonic oscillation. This means that spacetime has a physical structure and is therefore foamy on small scales. Applying our damped harmonic oscillator model to cosmology we rediscover the Friedman-Lemaitre equations for an expanding Universe. From the expanding Universe model we predict that cosmic acceleration, driven by an oscillating HSM and its gravitational interaction with a cosmic medium or Planck mass relics, manifests as the universe’s expansion accelerating over time, with a corresponding acceleration of roughly 10-10m/s2. Depending on the model, the “damping” aspect of the oscillator is interpreted as a constant dark gravity force which is also a representation of dark energy, a mysterious force causing the universe’s expansion to accelerate. We derive an estimate of the strength of this extra force in terms of the Gravitational constant, Planck mass, Hubble acceleration scale 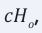
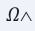
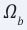
Keywords
• Dark Energy
• Cosmic Acceleration
• Expanding Universe
• String Theory
• Quantum Fluctuations
• Inflation
• Cosmology
• Large Scale Structures
• Density Perturbations
• Inflaton Field
Citation
Francis B (2025) On Spacetime as a Damped Harmonic Oscillator and The Dark Universe. J Phys Appl and Mech 2(2): 1011.
INTRODUCTION AND SUMMARY
According to Einstein’s theory of general relativity space-time has no physical structure other than its four dimensional continuum, essentially weaving space and time together as a single entity, with the structure of space-time being described by its curvature, which is influenced by the presence of mass and energy, causing massive objects to “bend” space- time around them; this curvature is what we perceive as gravity. This conventional point of view has been challenged by current theories and observations. From the observational side, the fact that 95% of our Universe consists of mysterious forms of energy or matter gives sufficient motivation to reconsider this basic starting point and from a theoretical perspective, insights from black hole physics and string theory indicate that our ‘macroscopic’ notions of space-time and gravity are emergent from an underlying microscopic description in which they have no a priori meaning [1].According to Wheeler and Nesterov [2,3], over sufficiently small distances and sufficiently brief intervals of time, the “very geometry of spacetime fluctuates”. These fluctuations could be large enough to cause significant departures from the smooth spacetime seen at macroscopic scales, giving spacetime a “foamy” character. This spacetime foam significantly impacts the effective cosmological constant, which is determined by the density of topological geons, implying that the source of dark energy is topological geons. Also according to Hinterbichler [4], one could hope to explain the acceleration of the universe without dark energy by choosing the graviton mass to be of order the Hubble constant.To differ from Wheeler and Nesterov [2,3], we present the structure of space-time as a damped oscillator of a Hubble Scale Mass (HSM) particle [5-9], in a viscous fluid [10], and using the equations of a simple harmonic oscillator as in classical physics, we show that the fabric of spacetime experiences oscillations that gradually decrease in amplitude over time, similar to how a physical object like a mass on a spring would lose energy and eventually come to rest when subject to a damping force; in this case, the “damping” would be caused by some mechanism within the spacetime itself that dissipates energy from the oscillations. Some potential mechanisms that could lead to such oscillations may include; dark energy dynamics and scalar fields [11]. Like any damped oscillation, the amplitude of the spacetime ripples would decrease exponentially with time, meaning the “waves” in spacetime would become smaller and smaller until they are negligible [11]. In cosmology, theories suggest that the early universe might have experienced a period of damped spacetime oscillations, potentially explaining the observed uniformity of the cosmic microwave background radiation (see section3). In quantum gravity frameworks, spacetime oscillations could be linked to the nature of quantum particles and their interactions [12,13]. The implication of space-time oscillations on cosmology is that if space undergoes damped oscillations, it could potentially affect our understanding of the universe’s ultimate fate, including whether it will continue to expand indefinitely or eventually collapse. Currently, there is no definitive observational evidence for a damped oscillating space- time of the universe, although some studies of distant supernovae and the cosmic microwave background radiation could potentially provide hints about past fluctuations in the expansion rate [14]. The aim of this paper is therefore to prove that space time is undergoing a damped oscillation and that the cause of this oscillation is attributed to the dynamics of the dark force.
The goal of this paper is to give a completely satisfactory microscopic description of space-time with a negative pressure and a positive cosmological constant to fully explain the cause of an accelerating expansion of the Universe. In this paper we provide evidence for the fact that the observed dark energy, the phenomena currently attributed to dark matter and the damped oscillation of space-time have a common origin and are connected to the rotational motion of a Hubble scale mass particle of space-time in the present Universe. This paper is structured as follows: In section two we apply the classical equations of a simple harmonic oscillator to an oscillating Hubble scale mass version of space-time. From this model we calculate the angular frequency, damping ratio and exponential decay of the oscillator. In (section 2.1) we apply the differential equation of a HSM damped oscillator to cosmology. In section three we apply the classical equations of a simple harmonic oscillator to an oscillating Planck mass version of space-time with implications for the early Universe.
FIRST MODEL: OSCILLATION OF A HUBBLE SCALE MASS PARTICLE IN A VISCOUS FLUID
Consider any region of space in the Universe where a vacuum of space is defined by an oscillating Hubble Scale Mass Particle (HSM) with mass, 10-68 kg in a fluid or vacuum of viscous damping coefficient,
is the Planck mass [15]. The damping coefficient given results from the presence of a residual Planck mass in the vacuum of space and the damping is therefore caused by a negative gravitational attraction of a HSM with the cosmic medium of a residual Planck mass.The particle‘s oscillating mass and the damping coefficient are therefore proportional to the Hubble angular frequency scale 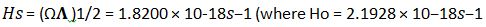
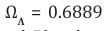
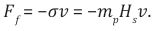
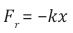
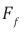
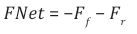
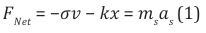
m and the cosmological constant
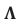
(where G, is the Gravitational constant).Putting in the values of the viscous damping coefficient
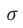
Writing this as a differential equation [17] in × , we obtain
This can be rewritten into the form [18-21]
From which the undamped angular frequency of the oscillator is given by an equation,
(Where Rs=
is the Schwarzschild radius of a HSM particle).The damping ratio is calculated to be,
This value of the damping ratio determines the behavior of the system.The exponential decay of the damped harmonic oscillator is given by,
The value 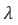
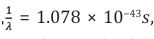
Application of First Model to Cosmology
Let the frictional force be a repulsive gravitational force resulting from an interaction of a HSM particle with the Planck mass. Because friction or damping is always in a direction to oppose the motion, this leads to a large negative pressure within the interaction. Therefore the large negative pressure P has repulsive gravity and can lead to the observed accelerated expansion of the universe. If we consider a small area of the vacuum of space, the frictional force or repulsive gravity acting perpendicular on the area A is the negative pressure P and is given by a simple equation,
structure constant or electromagnetic coupling constant, 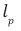
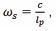
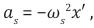
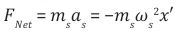
When the allowed calculable area for any region of space due to the foamy nature of space-tim (space-time foam, [22]) is 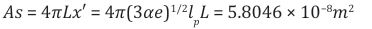
For an accelerating expansion of the Universe, the R.H.S of the above model equation shows that, the Hubble length scale takes on a new length scale 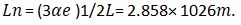
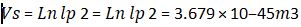
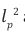
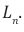
It is also worth noting that our model predicts cosmic acceleration at large cosmic length scales as,
is the value of cosmic acceleration of the observable Universe. The cosmic acceleration, driven by an oscillating HSM and it‘s gravitational attraction with a cosmic medium or Planck mass relics, manifests as the universe’s expansion accelerating over time, with a Hubble parameter
According to the equation given above, 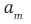
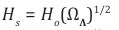
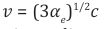
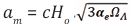
This means that there is no difference between an accelerating HSM and the cosmic medium presented by a residual Planck mass. Therefore the friction force or repulsive gravity that derives an accelerated expansion of the Universe is,
Where, h = 0.6755 , is the dimensionless reduced Hubble parameter. To be more precise, 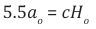
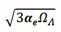
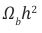
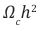
Notice here, 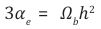
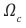
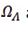
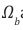
SECOND MODEL: OSCILLATION OF A PLANCK MASS-SIZED PARTICLE IN A VISCOUS FLUID
In this model, instead of an oscillating HSM we consider an oscillating Planck mass as described below. Let the system of space at any given point be described as an oscillating Planck mass particle with mass
Due to a frictional force, the velocity decreases in proportion to the acting frictional force.
The force constant or spring constant k is here proportional to the product of the Planck length and Cosmological constant as, Therefore the net force on the mass mp is:
Writing this as an equation in mass m, acceleration a, velocity v and displacement, × we obtain,
(6) Putting in the values of the viscous damping coefficient 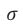
Writing this as a differential equation in × , we have
This can be rewritten into the form
From which the “undamped” angular frequency of oscillating space-time in the early universe had a value and a damping ratio of,
The exponential decay of this damped harmonic oscillator is given by
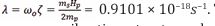
APPLICATION OF SECOND MODEL TO COSMOLOGY
Let the frictional force be a repulsive gravitational force resulting from an interaction of a Planck mass with a HSM particle. Because friction or damping is always in a direction to oppose the motion, this leads to a large negative pressure within the interaction. Therefore the large negative pressure P has repulsive gravity and can lead to the observed accelerated expansion of the universe. If we consider a small area of the vacuum of space, the frictional force or repulsive gravity acting perpendicular on the area A is the negative pressure P and is given by a simple equation, 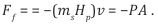
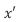
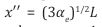
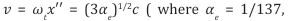
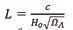
is the angular frequency or natural frequency of a simple harmonic oscillator of a Planck mass particle).
CONCLUSION
The idea of space-time as a damped oscillator is an intriguing concept that emerges from certain theoretical frameworks in physics, blending classical mechanics with cosmology or quantum gravity. Let‘s break it down naturally. is Imagine space-time as a kind of fabric that vibrates, much like a guitar string or a spring. In a damped oscillator, those vibrations don‘t go on forever-they fade out over time due to some kind of friction or energy loss. In the context of space-time, this could suggest that the universe‘s expansion, curvature, or even gravitational waves might behave like oscillations that gradually wind down. The “damping” could come from energy being dissipated into matter, radiation, or some exotic field. One place this idea might connect is cosmology. The universe‘s expansion seems to accelerate due to dark energy, but if we flip the script, a damped model might imply a universe that once oscillated more violently (see section3)-say, during the Big Bang-and is now settling into a quieter state (see section2). Think of the cosmic microwave background as a faint echo of that early “ringing” of space-time, damped by billions of years of expansion and cooling In quantum gravity or string theory, space-time could also oscillate at tiny scales. Some physicists speculate that space-time isn‘t perfectly smooth but has a foamy, vibrating structure. If those vibrations lose energy— maybe to virtual particles popping in and out of existence it‘s not hard to picture a damped oscillator-like behavior at the Planck scale. General relativity treats space-time as a smooth, dynamic geometry shaped by mass and energy, not a mechanical oscillator. To make the damped oscillator idea rigorous, you‘d need a model specifying what‘s oscillating (space-time metric? a scalar field?) and what‘s doing the damping (viscosity of the vacuum? interaction with a cosmic medium?). This study has clearly shown that oscillating HSM and its gravitational interaction with a cosmic medium or Planck mass relics, manifests as the universe’s expansion accelerating over time, with a corresponding acceleration of roughly 10−10m/s2. Depending on the model, the “damping” aspect of the oscillator is interpreted as a constant dark gravity force which is also a representation of dark energy, a mysterious force causing the universe’s expansion to accelerate.
DISCLAIMER
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
REFERENCES
- Verlinde EP. Emergent gravity and the dark universe. SciPost Physics.2017; 2: 16.
- Wheeler JA. Geon. Physical Review. 1955; 97: 511.
- Nesterov AI. Spacetime foam and solution of the cosmologicalconstant problem. 2024.
- Hinterbichler K. Theoretical aspects of massive gravity. 2011.
- Valev D. Evidence of dirac large numbers hypothesis. Proceedings ofthe Romanian Academy. 2019; 20: 361-368.
- Alfonso-Faus A. Universality of the self gravitational potential energyof any fundamental particle. Astrophys. Space Sci. 2012; 337: 363-365.
- Valev D. Neutrino and graviton rest mass estimations by aphenomenological approach. 2005; 21.
- Goldhaber AS, Nietto MM. Mass of the graviton. Physical Review D.1974; 9: 1119-1121.
- Sabine H, Tobias M. The redshift-dependence of radial acceleration:Modified gravity versus particle dark matter. 2018.
- Arbab AI. Matter aspect of the space-time: A viscous fluid. 2021.
- Khoshsima M. Universe, a spacetime harmonic oscillator. Int JPhysics. 2016; 4: 21-25.
- Macken JA. Oscillating spacetime: The foundation of the universe. JModern Physics. 2024; 15: 2024.
- Ng YJ, Dam HV.Measuring the foaminess of space-time with gravity-wave interferometers. 2000.
- DESI Collaboration, Adame AG, Aguilar J. Ahlen S, Alam S, Alexander DM, et al. DESI 2024 VI: cosmological constraints from the measurements of baryon acoustic oscillations. Cosmology and Nongalactic Astrophysics. 2024.
- CODATA Value: Planck mass. The NIST Reference on Constants, Units,and Uncertainty. 2022.
- The Planck Collaboration: Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck 2018 results. VI. Cosmological parameters. Astronomy and Astrophysics. 2021; 641.
- Rahman J, Mushtaq M, Ali A, Anjam YN, Nazir S. Modelling damped mass spring system in MATHLAB Simulink. J Faculty Engineering Technol. 2014; 21.
- Hayek SI. Mechanical vibration and damping. Encyclopedia of AppliedPhysics. 2003.
- Fowles, Grant R. Analytic Mechanics (5th ed), Fort Worth: Saunders College Publishing. 1999.
- Kreyszig, Erwin. Advanced Engineering Mathematics (3rd ed), NewYork. 1972.
- Rahman J, Mushtaq M, Ali A, Anjam YN, Nazir S. Modelling damped mass spring system in MATHLAB Simulink. J Faculty Engineering Technol. 2014; 21.
- Ng YJ. Measuring the foaminess of space-time with gravity-waveinterferometers. 2000.
- Milgrom M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys J. 1983; 270: 365-370.
- Milgrom M. A modification of the Newtonian dynamics - Implications for galaxies. 1983; 270: 371-383.