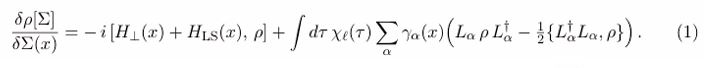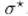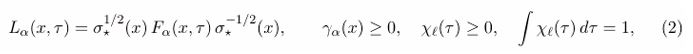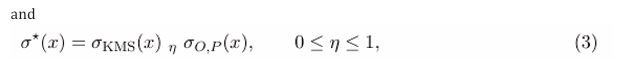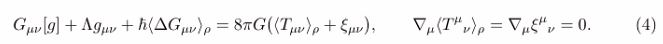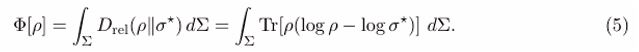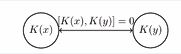The Universal Refined Equation (CUP-Ω*): Covariant GKLS Dynamics, Tomonaga–Schwinger Integrability, and Einstein Langevin Coupling in the CUCE/ Spinoza/Hilbert Framework
- 1. Campo Unificado de la Consciencia–Existencia (CUCE), Finis Terrae University, Chile
Abstract
We present a covariant, completely positive and thermodynamically consistent refinement of the universal equation within the CUCE/Spinoza/Hilbert framework, denoted CUP-?*. The formulation unifies Tomonaga–Schwinger evolution on Cauchy hypersurfaces with a modular Gorini–Kossakowski–Lindblad Sudarshan (GKLS) generator that obeys detailed balance in the GNS metric with respect to a unified thermodynamic target σ*. We prove (i) foliation independence under local commutation, (ii) complete positivity of the finite-step propagator, (iii) existence of a global Lyapunov functional 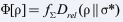
Keywords
• Covariant Open Quantum Systems; Quantum Markov Semigroups; Detailed Balance; Tomonaga Schwinger Equation; Stochastic Gravity; Information Geometry; Thermodynamic Learning 1
Citation
Gallardo VM (2026) The Universal Refined Equation (CUP-?*): Covariant GKLS Dynamics, Tomonaga–Schwinger Integrability, and Ein stein–Langevin Coupling in the CUCE/Spinoza/Hilbert Framework. J Phys Appl and Mech 3(1): 1016.
INTRODUCTION
Spinoza’s monism can be operationally reformulated in Hilbert-space language: one substance, many modes as observable algebras. Within this CUCE/Spinoza/Hilbert programme, the CUP-?∗ equation supplies a universal dynamical law that is (a) covariant at the level of foliation by Cauchy hypersurfaces, (b) completely positive at finite steps, and (c) thermodynamically consistent via a modular target 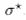
MAIN EQUATION
Let ρ[Σ] be the state functional on a Cauchy hypersurface Σ. The local Tomonaga–Schwinger (TS) evolution at x ∈ Σ reads
The jump operators are modular with respect to the unified thermodynamic target
Where denotes the affine geometric mean. Equation (1) couples to semiclassical gravity via a conserved stochastic source through
Axioms
(Causal) Local commutation. For spacelike separated x, y, the local superoperators commute: 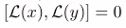
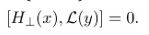
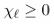
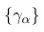
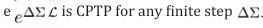
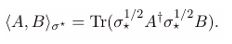
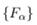
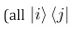
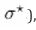
(Cons) Conservation and gauge. Fα are BRST-invariant; (4) uses conserved noise with fluctuation–dissipation relations.
Global Lyapunov functional and the second law
Theorem 1 (Monotonicity and exponential convergence). Under axioms (GNS) and (CPTP), 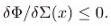
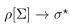
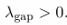
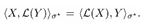
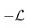
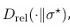
Finite-step complete positivity
Theorem 2 (Finite-step CPTP). 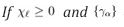
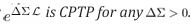
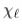
Primitivity and uniqueness of the attractor
Theorem 3 (Unique fixed point). If 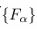
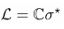
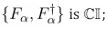
TS integrability and causality
Theorem 4 (Foliation independence). If 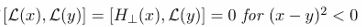
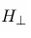
Proof. Adapt Schwinger’s argument: local commutators integrate to zero over spacelike-separated elements, ensuring path-independence of the ordered exponential along deformations of Σ.
Conservation and Einstein–Langevin coupling
Theorem 5 (Local conservation). With conserved noise 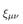
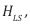
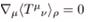
Falsifiability and quantitative predictions
We outline protocols that access the modular structure and the conserved stochastic back-reaction:
1. Entropy production bound in a qubit. Engineering {Fa} to be the full set of matrix units on a superconducting qubit makes the dynamics primitive. The relative-entropy half-life obeys 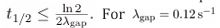
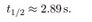
2. For Equilibrium test of the unified target. For a 5 GHz qubit at T = 50 mK, the KMS factor is 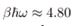
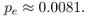
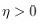
3. Choi test of finite-step CPTP. Reconstruct the Choi matrix of the propagator over a finite TS “slab”; positivity must hold within uncertainties fixed by the noise kernel.
4. Optomechanical probe of conserved noise. For a membrane of mass 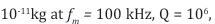
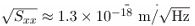
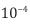
Limiting regimes
The principal asymptotic limits of CUP-?∗ and the corresponding recovered theories are summa- rized in Table 1.
Figures (TikZ/PGFPlots)
METHODS
GNS detailed balance and modular jumps. Choosing 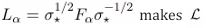
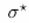
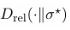
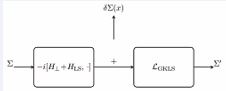
Figure 1 Local TS block: unitary plus modular GKLS applied on a surface element.
Finite-step CPTP with Bochner kernels. Bochner positivity guarantees the Kossakowski matrix is positive semidefinite; the finite-step propagator is a convex mixture of infinitesimal CPTP maps, hence CPTP (Figure 2).
Figure 2 Local integrability under spacelike separation..
Einstein–Langevin consistency. Conserved noise ensures 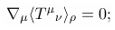
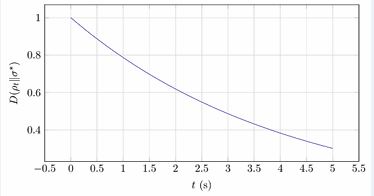
Figure 3 Typical Lyapunov descent of relative entropy with rate bound 2λgap.
Data availability: No datasets were generated or analysed for this theoretical study.
Code Availability: All LaTeX/TikZ/PGFPlots code to reproduce the manuscript is included in the accompanying project.
Author Contributions: VMG conceived the CUP-?∗ framework, developed the mathematical proofs and wrote the manuscript.
Acknowledgements
We thank the broader communities working on GKLS dynamics, information geometry and stochastic gravity for foundational insights.
REFERENCES
- Carlen EA, Jan Maas. Gradient flow and entropy inequalities for quantum markov semigroups with detailed balance. J Functional Analysis. 2017; 273: 1810-1869.
- Gorini V, Kossakowski A, Sudarshan ECG. Completely positive dynamical semigroups of n-level systems. J Mathematical Physics. 1976; 17: 821-825.
- Lindblad G. On the generators of quantum dynamical semigroups. Communications in Mathematical Physics. 1976; 48: 119-130.